题目内容
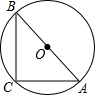 如图,AB是⊙O的直径,AC=BC,则∠A=
如图,AB是⊙O的直径,AC=BC,则∠A=考点:圆周角定理,等腰直角三角形
专题:
分析:先由AB是⊙O的直径得出∠C=90°,再根据AC=BC,得出△ABC是等腰直角三角形,由此求出∠A=45°.
解答:解:∵AB是⊙O的直径,
∴∠C=90°,
∵AC=BC,
∴△ABC是等腰直角三角形,
∴∠A=∠B=
(180°-∠C)=45°.
故答案为45.
∴∠C=90°,
∵AC=BC,
∴△ABC是等腰直角三角形,
∴∠A=∠B=
| 1 |
| 2 |
故答案为45.
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.同时考查了等腰直角三角形的性质.

练习册系列答案
相关题目
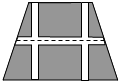 如图,要设计一个等腰梯形的花坛,花坛上底长120米,下底长180米,上下底相距80米,在两腰中点连线(虚线)处有一条横向甬道,上下底之间有两条纵向甬道,各甬道的宽度相等.设甬道的宽为x米.
如图,要设计一个等腰梯形的花坛,花坛上底长120米,下底长180米,上下底相距80米,在两腰中点连线(虚线)处有一条横向甬道,上下底之间有两条纵向甬道,各甬道的宽度相等.设甬道的宽为x米.