题目内容
用合适的方法解下列方程:
(1)(2x-1)2-25=0;
(2)3x2=2x;
(3)2a2-5a+1=0.
(1)(2x-1)2-25=0;
(2)3x2=2x;
(3)2a2-5a+1=0.
考点:解一元二次方程-因式分解法,解一元二次方程-直接开平方法,解一元二次方程-公式法
专题:
分析:(1)先根据平方差公式分解因式,即可得出两个一元一次方程,求出方程的解即可;
(2)移项后分解因式,即可得出两个一元一次方程,求出方程的解即可;
(3)求出b2-4ac的值,代入公式求出即可.
(2)移项后分解因式,即可得出两个一元一次方程,求出方程的解即可;
(3)求出b2-4ac的值,代入公式求出即可.
解答:解:(1)(2x-1)2-25=0,
(2x-1+5)(2x-1-5)=0,
2x-1+5=0,2x-1-5=0,
x1=-2,x2=3;
(2)3x2=2x,
3x2-2x=0,
x(3x-2)=0,
x=0,3x-2=0,
x1=0,x2=
;
(3)2a2-5a+1=0,
△=(-5)2-4×2×1=17,
a=
,
a1=
,a2=
.
(2x-1+5)(2x-1-5)=0,
2x-1+5=0,2x-1-5=0,
x1=-2,x2=3;
(2)3x2=2x,
3x2-2x=0,
x(3x-2)=0,
x=0,3x-2=0,
x1=0,x2=
| 2 |
| 3 |
(3)2a2-5a+1=0,
△=(-5)2-4×2×1=17,
a=
5±
| ||
| 2×2 |
a1=
5+
| ||
| 4 |
5-
| ||
| 4 |
点评:本题考查了解一元二次方程的应用,主要考查学生能否选择适当的方法解一元二次方程.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
 如图是由一些相同的小正方体构成的立体图形分别从正面、左面、上面看到的形状图.那么构成这个立体图形的小正方体有( )
如图是由一些相同的小正方体构成的立体图形分别从正面、左面、上面看到的形状图.那么构成这个立体图形的小正方体有( )| A、4个 | B、5个 | C、6个 | D、7个 |
一元二次方程5(x2+1)-7x=0( )
| A、有两个不相等的实数根 |
| B、有两个相等实数根 |
| C、只有一个实数根 |
| D、没有实数根 |
方程x2=1的根是( )
| A、x=1 | B、x=-1 |
| C、x=±1 | D、以上答案都不对 |
 两圆的位置关系有多种.图中不存在的位置关系是
两圆的位置关系有多种.图中不存在的位置关系是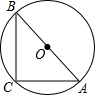 如图,AB是⊙O的直径,AC=BC,则∠A=
如图,AB是⊙O的直径,AC=BC,则∠A=