题目内容
18. 如图,在平面直角坐标系中,∠OCA=90°,点A在x轴上,OC=AC=4,D、E分别是OC、AC的中点,将四边形OAED沿x轴向右平移,得四边形PQRS.设OP=m(0<m<4$\sqrt{2}$).
如图,在平面直角坐标系中,∠OCA=90°,点A在x轴上,OC=AC=4,D、E分别是OC、AC的中点,将四边形OAED沿x轴向右平移,得四边形PQRS.设OP=m(0<m<4$\sqrt{2}$).(Ⅰ)在平移过程中,四边形OPSD能否成为菱形?若能,求出此时m的值;若不能,说明理由.
(Ⅱ)设平移过程中△OAC与四边形SPQR重叠部分的面积为S,试用含m的式子表示S.
(Ⅲ)当S=3时,求点P的坐标(直接写出结果即可)
分析 (1)根据平移得到OD∥PS,OD=PS,再由菱形的判定方法有OP=OD,即可;
(2)分两段求出面积,①当0<m<2$\sqrt{2}$时,先表示出SE=2$\sqrt{2}$-m,PA=4$\sqrt{2}$-m,重叠部分为梯形PAES,求出即可,②当2$\sqrt{2}$≤m<4$\sqrt{2}$时,重叠部分为△PAN,再求出此三角形的底和高即可;
(3)由(2)的函数关系式,分别代S=3,解出m,判断即可.
解答 解:(Ⅰ)能为菱形,
理由:由平移知,OD∥PS,OD=PS,
∴四边形OPSD是平行四边形,
当OP=OD时,四边形OPSD能为菱形,
∵D是OC中点,OC=4,
∴OD=$\frac{1}{2}$OC=2,
∴OP=2,
即:m=2时,四边形OPSD是菱形;
(Ⅱ)①当0<m<2$\sqrt{2}$时,重叠部分为梯形PAES,
如图,
作DH⊥OA,
∵D,E分别是OC,AC中点,OD=2,
∴DH=$\sqrt{2}$,DE=$\frac{1}{2}$OA=2$\sqrt{2}$,
∵DS=OP=m
∴SE=2$\sqrt{2}$-m,PA=4$\sqrt{2}$-m,
S=$\frac{1}{2}$(SE+PA)×DH
=$\frac{1}{2}$[(2$\sqrt{2}$-m)+(4$\sqrt{2}$-m)]×$\sqrt{2}$
=6-$\sqrt{2}$m,(0<m<2$\sqrt{2}$)
②当2$\sqrt{2}$≤m<4$\sqrt{2}$时,PS与AC相交于N,重叠部分为△PAN,
∵△PAN为等腰直角三角形,
∴PA=4$\sqrt{2}$-m,△PAN的PA边上的高h=$\frac{1}{2}$(4$\sqrt{2}$-m),
∴S=$\frac{1}{2}$PA×h
=$\frac{1}{2}$(4$\sqrt{2}$-m)×$\frac{1}{2}$(4$\sqrt{2}$-m)
=$\frac{1}{4}$m2-2$\sqrt{2}$m+8(2$\sqrt{2}$≤m<4$\sqrt{2}$);
(Ⅲ)∵S=3,
∴①当0<m<2$\sqrt{2}$时,6-$\sqrt{2}$m=3,
∴m=$\frac{3\sqrt{2}}{2}$,
∴P($\frac{3\sqrt{2}}{2}$,0)
②当2$\sqrt{2}$≤m<4$\sqrt{2}$时,$\frac{1}{4}$m2-2$\sqrt{2}$m+8=3,
∴m2-8$\sqrt{2}$m+20=0,
∴m=4$\sqrt{2}$+2$\sqrt{3}$(舍),或m=4$\sqrt{2}$-2$\sqrt{3}$(舍)
即:P($\frac{3\sqrt{2}}{2}$,0).
点评 此题是四边形综合题,主要考查了菱形的性质和判定,等腰直角三角形的性质,梯形,三角形的面积计算方法,解本题的关键是求出重叠部分面积和点P的横坐标m的关系.

 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案 如图,菱形ABCD的两条对角线相交于点O,若AC=8cm,BD=6cm,求菱形的面积和周长各是多少?
如图,菱形ABCD的两条对角线相交于点O,若AC=8cm,BD=6cm,求菱形的面积和周长各是多少? 二次函数y=ax2+bx+c的图象如图所示,反比例函数y=$\frac{a}{x}$与正比例函数y=bx在同一坐标系中的大致图象可能是( )
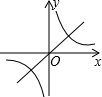
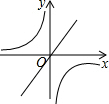
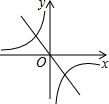
二次函数y=ax2+bx+c的图象如图所示,反比例函数y=$\frac{a}{x}$与正比例函数y=bx在同一坐标系中的大致图象可能是( )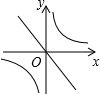
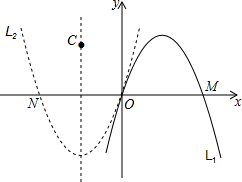 在直角坐标系xOy中,定义点C(a,b)为抛物线L:y=ax2+bx(a≠0)的特征点坐标.
在直角坐标系xOy中,定义点C(a,b)为抛物线L:y=ax2+bx(a≠0)的特征点坐标.
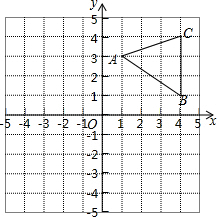 如图,已知△ABC,第一次作△ABC绕点O按逆时针旋转90°后得到△A1B1C1,第二次作△A1B1C1关于x轴对称的图形△A2B2C2,在以下坐标系中作出△A1B1C1、△A2B2C2,并求对应点A2的坐标(-3,-1).
如图,已知△ABC,第一次作△ABC绕点O按逆时针旋转90°后得到△A1B1C1,第二次作△A1B1C1关于x轴对称的图形△A2B2C2,在以下坐标系中作出△A1B1C1、△A2B2C2,并求对应点A2的坐标(-3,-1).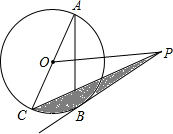 已知:如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点.∠PBA=∠ACB.
已知:如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点.∠PBA=∠ACB.