题目内容
9. 如图,菱形ABCD的两条对角线相交于点O,若AC=8cm,BD=6cm,求菱形的面积和周长各是多少?
如图,菱形ABCD的两条对角线相交于点O,若AC=8cm,BD=6cm,求菱形的面积和周长各是多少?
分析 根据菱形的性质可得AO=OC=4,DO=BO=3,根据勾股定理求出AD,根据菱形的面积等于对角线乘积的一半,由此即可解决问题.
解答  解:∵四边形ABCD是菱形,
解:∵四边形ABCD是菱形,
∴AO=OC=4,BO=OD=3,AC⊥BD,AD=DC=BC=AB,
∴∠AOD=90°,
∴AD=$\sqrt{A{O}^{2}+D{O}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5,
∴菱形ABCD的周长为20,面积=$\frac{1}{2}$•AC•BD=24.
点评 本题考查菱形的性质,记住菱形的性质,菱形的对角线互相垂直平分,菱形的面积等于对角线乘积的一半,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.从-3,-1,0,2四个数中任选两个,则这两个数的乘积为负数的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
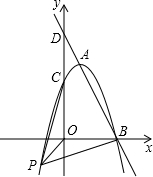 如图,已知直线y=kx+6与抛物线y=ax2+bx+c相交于A,B两点,且点A(1,4)为抛物线的顶点,点B在x轴上.
如图,已知直线y=kx+6与抛物线y=ax2+bx+c相交于A,B两点,且点A(1,4)为抛物线的顶点,点B在x轴上.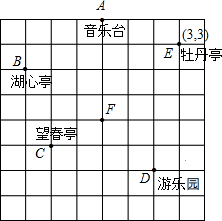 多多和爸爸、妈妈周末到公园游玩,回到家后,他利用平面直角坐标系画出了公园的景区地图,如图所示.可是他忘记了在图中标出原点和x轴、y轴.只知道牡丹园的坐标为(3,3),请你帮他建立平面直角坐标系(画在图中)并求出其它各景点的坐标?
多多和爸爸、妈妈周末到公园游玩,回到家后,他利用平面直角坐标系画出了公园的景区地图,如图所示.可是他忘记了在图中标出原点和x轴、y轴.只知道牡丹园的坐标为(3,3),请你帮他建立平面直角坐标系(画在图中)并求出其它各景点的坐标?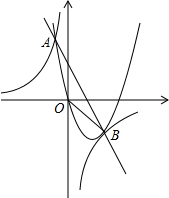 如图,直线y=-2x+2与抛物线y=ax2+bx(a<0)相交于点A,B.双曲线y=$\frac{k}{x}$过A、B两点,已知点B的坐标为(2,-2),点A在第二象限内,且tan∠Aoy=$\frac{1}{4}$.
如图,直线y=-2x+2与抛物线y=ax2+bx(a<0)相交于点A,B.双曲线y=$\frac{k}{x}$过A、B两点,已知点B的坐标为(2,-2),点A在第二象限内,且tan∠Aoy=$\frac{1}{4}$. 如图,在平面直角坐标系中,∠OCA=90°,点A在x轴上,OC=AC=4,D、E分别是OC、AC的中点,将四边形OAED沿x轴向右平移,得四边形PQRS.设OP=m(0<m<4$\sqrt{2}$).
如图,在平面直角坐标系中,∠OCA=90°,点A在x轴上,OC=AC=4,D、E分别是OC、AC的中点,将四边形OAED沿x轴向右平移,得四边形PQRS.设OP=m(0<m<4$\sqrt{2}$).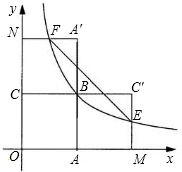 如图,四边形OABC是面积为4的正方形,函数y1=$\frac{k}{x}$(x>0)的图象经过点B.
如图,四边形OABC是面积为4的正方形,函数y1=$\frac{k}{x}$(x>0)的图象经过点B.