题目内容
14. 如图,在△ABC中,∠A=80°,∠ABC和∠ACD的平分线交于点E,则∠E=40°.
如图,在△ABC中,∠A=80°,∠ABC和∠ACD的平分线交于点E,则∠E=40°.
分析 利用角平分线定义可知∠ECD=$\frac{1}{2}$∠ACD.再利用外角性质,可得∠ACD=∠A+∠ABC①,∠ECD=∠E+$\frac{1}{2}$∠ABC②,那么可利用∠ECA=∠ECD,可得相等关系,从而可求∠E的度数.
解答 解:∵CE是∠ACD的角平分线,
∴∠ECD=$\frac{1}{2}$∠ACD.
又∵∠ACD=∠A+∠ABC,
∴∠ECD=$\frac{1}{2}$∠A+$\frac{1}{2}$∠ABC,
又∵∠ECD=∠E+$\frac{1}{2}$∠ABC,
∴$\frac{1}{2}$∠A+$\frac{1}{2}$∠ABC=∠E+$\frac{1}{2}$∠ABC,
∴∠E=$\frac{1}{2}$∠A=40°,
故答案为:40°.
点评 本题考查三角形外角的性质及三角形的内角和定理,解题的关键是熟记三角形的内角和.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
 如图已知△ABC,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,则图中的等腰三角形是3.
如图已知△ABC,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,则图中的等腰三角形是3.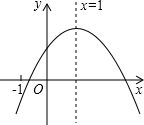 已知二次函数y=ax2+bx+c的图象如图所示,其对称轴为直线x=1,有下列结论:①abc>0;②b2<4ac;③(a+c)2>b2 ④a<$\frac{c-b}{2}$,其中正确结论的个数是( )
已知二次函数y=ax2+bx+c的图象如图所示,其对称轴为直线x=1,有下列结论:①abc>0;②b2<4ac;③(a+c)2>b2 ④a<$\frac{c-b}{2}$,其中正确结论的个数是( )