题目内容
6.已知二次函数图象的对称轴是3+x=0,图象经过(1,6),且与y轴的交点为(0,$\frac{5}{2}$).(1)求这个二次函数的解析式;
(2)当x为何值时,这个函数的函数值为0?
(3)当x在什么范围内变化时,这个函数的函数值y随x的增大而增大?
分析 (1)本题实际上已知了三个条件,可设抛物线的一般形式y=ax2+bx+c求解;
(2)将y=0代入(1)中所求的解析式,即可求解;
(3)利用二次函数的性质即可解答这个问题.
解答 解:(1)设抛物线的解析式为y=ax2+bx+c,
由题意可得$\left\{\begin{array}{l}{-\frac{b}{2a}=-3}\\{a+b+c=6}\\{c=\frac{5}{2}}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=3}\\{c=\frac{5}{2}}\end{array}\right.$,
所以这个二次函数的解析式为y=$\frac{1}{2}$x2+3x+$\frac{5}{2}$;
(2)令y=0,得$\frac{1}{2}$x2+3x+$\frac{5}{2}$=0,
解得:x=-1或5.
答:当x为-1或5时,这个函数的函数值为0;
(3)∵y=$\frac{1}{2}$x2+3x+$\frac{5}{2}$,
∴a=$\frac{1}{2}$>0,开口向上,对称轴是x=-3,
∴当x>-3时,函数的函数值y随x的增大而增大.
点评 本题考查了用待定系数法求二次函数解析式的方法,同时还考查了二次函数的性质等相关知识.

练习册系列答案
相关题目
1.抛物线y=x2向左平移8个单位,再向下平移9个单位后,所得抛物线的表达式是( )
| A. | y=(x+8)2-9 | B. | y=(x-8)2+9 | C. | y=(x-8)2-9 | D. | y=(x+8)2+9 |
16.数轴上表示整数的点称为整点,某数轴的单位长度为1cm,若在数轴上画出一条长2016cm的线段AB,则AB盖住的整点个数是( )
| A. | 2016或2017 | B. | 2015或2016 | C. | 2015 | D. | 2016 |
 如图,在△ABC中,∠B=70°,∠BAC=45°,AD⊥BC于点D,则∠CAD的度数为25°.
如图,在△ABC中,∠B=70°,∠BAC=45°,AD⊥BC于点D,则∠CAD的度数为25°. 如图,在△ABC中,∠A=80°,∠ABC和∠ACD的平分线交于点E,则∠E=40°.
如图,在△ABC中,∠A=80°,∠ABC和∠ACD的平分线交于点E,则∠E=40°.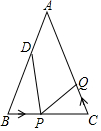 如图,已知△ABC中,AB=AC=18cm,∠B=∠C,BC=12cm,点D为AB的中点.
如图,已知△ABC中,AB=AC=18cm,∠B=∠C,BC=12cm,点D为AB的中点. 如图,在等腰Rt△ABC中,∠BAC=90°.将直角边足够长的Rt△EPF的直角顶点P放在线段BC的中点上,以点P为旋转中心,转动Rt△EPF并使它的两直角边PE,PF分别与AC,AB相交于点N,M,连MN,AP,交于D点,则下列几组量:
如图,在等腰Rt△ABC中,∠BAC=90°.将直角边足够长的Rt△EPF的直角顶点P放在线段BC的中点上,以点P为旋转中心,转动Rt△EPF并使它的两直角边PE,PF分别与AC,AB相交于点N,M,连MN,AP,交于D点,则下列几组量: