题目内容
9. 如图已知△ABC,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,则图中的等腰三角形是3.
如图已知△ABC,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,则图中的等腰三角形是3.
分析 由已知条件,利用三角形的内角和定理及角平分线的性质得到各角的度数,根据等腰三角形的定义及等角对等边得出答案.
解答 解:∵AB=AC,∴△ABC是等腰三角形.
∵∠A=36°,∴∠C=∠ABC=72°.
BD平分∠ABC交AC于D,
∴∠ABD=∠DBC=36°,
∵∠A=∠ABD=36°,
∴△ABD是等腰三角形.
∠BDC=∠A+∠ABD=36°+36°=72°=∠C,
∴△BDC是等腰三角形.
∴共有3个等腰三角形.
故答案为:3
点评 本题考查了等腰三角形的判定与性质及三角形内角和定理;求得角的度数是正确解答本题的关键.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
1.抛物线y=x2向左平移8个单位,再向下平移9个单位后,所得抛物线的表达式是( )
| A. | y=(x+8)2-9 | B. | y=(x-8)2+9 | C. | y=(x-8)2-9 | D. | y=(x+8)2+9 |
19.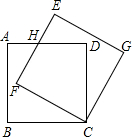 如图,边长为$\sqrt{3}$的正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG,EF交AD于点H,则四边形DHFC的面积为( )
如图,边长为$\sqrt{3}$的正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG,EF交AD于点H,则四边形DHFC的面积为( )
 如图,边长为$\sqrt{3}$的正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG,EF交AD于点H,则四边形DHFC的面积为( )
如图,边长为$\sqrt{3}$的正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG,EF交AD于点H,则四边形DHFC的面积为( )| A. | $\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | 9 | D. | 6$\sqrt{3}$ |
 在三角形MNQ中.
在三角形MNQ中. 如图,在△ABC中,∠B=∠C,∠BAD=34°,且∠ADE=∠AED,则∠CDE=17度.
如图,在△ABC中,∠B=∠C,∠BAD=34°,且∠ADE=∠AED,则∠CDE=17度. 如图,在△ABC中,∠A=80°,∠ABC和∠ACD的平分线交于点E,则∠E=40°.
如图,在△ABC中,∠A=80°,∠ABC和∠ACD的平分线交于点E,则∠E=40°.