题目内容
6.观察:(x-1)(x+1)=x2-1,(x-1)(x2+x+1)=x3-1,(x-1)(x3+x2+x+1)=x4-1,…(1)按以上规律直接写出:(x-1)(x5+x4+x3+x2+x+1)=x6-1,(x-1)(xn+xn-1+…+x+1)=xn+1-1
(2)利用(1)中的结论,尝试计算:1+2+22+23+…+250.(写出解答过程)
分析 (1)根据已知等式确定出所求式子的结果即可;
(2)原式变形后,利用得出的规律计算即可得到结果.
解答 解:(1)(x-1)(x5+x4+x3+x2+x+1)=x6-1,(x-1)(xn+xn-1+…+x+1)=xn+1-1;
(2)原式=(2-1)(1+2+22+23+…+250)=251-1.
故答案为:(1)x6-1;xn+1-1.
点评 此题考查了平方差公式,熟练掌握平方差公式是解本题的关键.

练习册系列答案
相关题目
16.“十一”黄金周期间,宿迁市某公园在七天假期中每天旅游人变化数变化如下:(正数表示比前一天多的人数,负数表示比前一天少的人数).
(单位:万人)
(1)若9月30日游客人数为3万人,10月2日的游客人数是多少人?
(2)请判断7天内游客最多的人数是哪天?最少的人数是哪天?求这一次黄金周期间游客在该地的总人数.
(单位:万人)
| 日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
| 人数变化 | +1.6 | +0.4 | +1 | -0.5 | -0.8 | +0.2 | -1.2 |
(2)请判断7天内游客最多的人数是哪天?最少的人数是哪天?求这一次黄金周期间游客在该地的总人数.
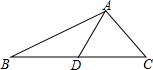 如图,△ABC中,D是BC上一点,AC=AD=DB,∠BAC=105°,则∠ADC=50°.
如图,△ABC中,D是BC上一点,AC=AD=DB,∠BAC=105°,则∠ADC=50°.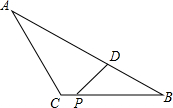 如图,在△ABC中,AB=6,BC=4,AC=3,点P在边BC上运动(不含点B),过点P作∠DPB=∠A,PD交AB于点D吗,设PB=x,AD=y
如图,在△ABC中,AB=6,BC=4,AC=3,点P在边BC上运动(不含点B),过点P作∠DPB=∠A,PD交AB于点D吗,设PB=x,AD=y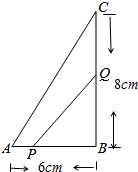 如图,△ABC中,∠B=90°,点P从A点开始沿AB向点B以1cm/s的速度移动,点Q从B点开始沿BC向点C以2cm/s的速度移动,当一方停止运动时另一方也随之停止运动.
如图,△ABC中,∠B=90°,点P从A点开始沿AB向点B以1cm/s的速度移动,点Q从B点开始沿BC向点C以2cm/s的速度移动,当一方停止运动时另一方也随之停止运动. 如图,某公路上有A、B、C三站,一辆汽车在上午8时从高A站5km的P地出发向C站匀速行驶,15min后离A站20km
如图,某公路上有A、B、C三站,一辆汽车在上午8时从高A站5km的P地出发向C站匀速行驶,15min后离A站20km