题目内容
16.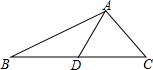 如图,△ABC中,D是BC上一点,AC=AD=DB,∠BAC=105°,则∠ADC=50°.
如图,△ABC中,D是BC上一点,AC=AD=DB,∠BAC=105°,则∠ADC=50°.
分析 设∠ADC=α,然后根据AC=AD=DB,∠BAC=105°,表示出∠B和∠BAD的度数,最后根据三角形的内角和定理求出∠ADC的度数.
解答 解:∵AC=AD=DB,
∴∠B=∠BAD,∠ADC=∠C,
设∠ADC=α,
∴∠B=∠BAD=$\frac{α}{2}$,
∵∠BAC=105°,
∴∠DAC=105°-$\frac{α}{2}$,
在△ADC中,
∵∠ADC+∠C+∠DAC=180°,
∴2α+105°-$\frac{α}{2}$=180°,
解得:α=50°.
故答案为:50.
点评 本题考查了等腰三角形的性质:①等腰三角形的两腰相等;②等腰三角形的两个底角相等,熟练掌握等腰三角形的性质是解题的关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
6.将抛物线y=2x2向左平移2个单位,得到的抛物线是( )
| A. | y=2(x+2)2 | B. | y=2(x-2)2 | C. | y=2x2+2 | D. | y=2x2-2 |
11.树的高度与树生长的年数有关,测得某棵树的有关数据如下表(树苗原高80厘米):
(1)填出第4年树苗可能达到的高度;
(2)请用含a的代数式表示:a年后树的高度h=7a+80;
(3)根据这种长势,12年后这棵树可能达到的高度是164厘米.
| 年数a | 高度h(单位:厘米) |
| 1 | 87 |
| 2 | 94 |
| 3 | 101 |
| 4 | 108 |
| … | … |
(2)请用含a的代数式表示:a年后树的高度h=7a+80;
(3)根据这种长势,12年后这棵树可能达到的高度是164厘米.
8.当x=1时,代数式ax3+bx+1的值为6,当x=-1时,代数式ax3+bx+1的值等于( )
| A. | 0 | B. | -3 | C. | -4 | D. | -5 |



