题目内容
8.先化简,然后再选一个合适的x值代入,求值:$(\frac{x+2}{{{x^2}-2x}}-\frac{x-1}{{{x^2}-4x+4}})÷\frac{{{x^2}-16}}{{{x^2}+4x}}$.分析 先根据分式混合运算的法则把原式进行化简,再选择合适的x的值代入进行计算即可.
解答 解:原式=($\frac{x+2}{x(x-2)}$-$\frac{x-1}{(x-2)^{2}}$)÷$\frac{x-4}{x}$
=$\frac{{x}^{2}-4-{x}^{2}+x}{x{(x-2)}^{2}}$•$\frac{x}{x-4}$
=$\frac{x-4}{x{(x-2)}^{2}}$•$\frac{x}{x-4}$
=$\frac{1}{{(x-2)}^{2}}$,
当x=3时,原式=1.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
18.在平面直角坐标系中,点P(3,-x2-1)所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
18.已知线段QP,AP=AQ,以QP为直径作圆,点A与此圆的位置关系是( )
| A. | 点A在圆内 | B. | 点A在圆上 | C. | 点A在圆外 | D. | 不能确定 |
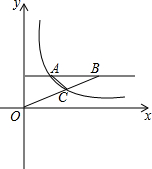 如图,反比例函数y=$\frac{6}{x}$(x>0)上任取一点A,过A作AB∥x轴,OB交图象于C,OC:BC=2:3,求△ABC面积.
如图,反比例函数y=$\frac{6}{x}$(x>0)上任取一点A,过A作AB∥x轴,OB交图象于C,OC:BC=2:3,求△ABC面积.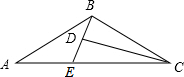 如图,D为△ABC内一点,CD平分∠ACB,BE⊥CD,垂足为D,交AC于点E,∠A=∠ABE,AC=5,BC=3,则BD的长为( )
如图,D为△ABC内一点,CD平分∠ACB,BE⊥CD,垂足为D,交AC于点E,∠A=∠ABE,AC=5,BC=3,则BD的长为( )