题目内容
17.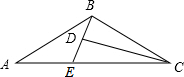 如图,D为△ABC内一点,CD平分∠ACB,BE⊥CD,垂足为D,交AC于点E,∠A=∠ABE,AC=5,BC=3,则BD的长为( )
如图,D为△ABC内一点,CD平分∠ACB,BE⊥CD,垂足为D,交AC于点E,∠A=∠ABE,AC=5,BC=3,则BD的长为( )| A. | 1 | B. | 1.5 | C. | 2 | D. | 2.5 |
分析 由已知条件判定△BEC的等腰三角形,且BC=CE;由等角对等边判定AE=BE,则易求BD=$\frac{1}{2}$BE=$\frac{1}{2}$AE=$\frac{1}{2}$(AC-CE).
解答 解:∵CD平分∠ACB,BE⊥CD,
∴BC=CE.
又∵∠A=∠ABE,
∴AE=BE.
∴BD=$\frac{1}{2}$BE=$\frac{1}{2}$AE=$\frac{1}{2}$(AC-BC).
∵AC=5,BC=3,
∴BD=$\frac{1}{2}$(5-3)=1.
故选A.
点评 本题考查了等腰三角形的判定与性质.注意等腰三角形“三线合一”性质的运用.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
7.下列运算中,正确的是( )
| A. | 3a2-a2=2 | B. | (-a2b)3=a6b3 | C. | a3•a6=a9 | D. | (2a2)2=2a4 |
5.下列计算中,正确的是( )
| A. | $\sqrt{9}$=±3 | B. | (-$\frac{1}{3}$)-1=-3 | C. | 2a+3b=5ab | D. | a6÷a2=a3 |
2.下列命题错误的是( )
| A. | 对角线相互平分的四边形是平行四边形 | |
| B. | 对角线相互平分且相等的四边形是矩形 | |
| C. | 对角线相互平分且垂直的四边形是菱形 | |
| D. | 对角线相等且垂直的四边形是正方形 |
9.下列各运算中,计算正确的是( )
| A. | 3x2+5x2=8x4 | B. | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{6}$ | ||
| C. | $\frac{1}{x+1}$-$\frac{1}{x-1}$=$\frac{2}{{{x^2}-1}}$ | D. | (-$\frac{1}{2}$m2n)2=$\frac{1}{4}$m4n2 |
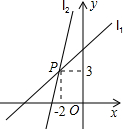 如图,一次函数y=k1x+b1的图象l1与y=k2x+b2的图象l2相交于点P,则关于x的不等式k1x+b1>k2x+b2的解集是x<-2.
如图,一次函数y=k1x+b1的图象l1与y=k2x+b2的图象l2相交于点P,则关于x的不等式k1x+b1>k2x+b2的解集是x<-2.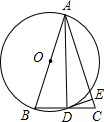 (1)如图,在△ABC中,以AB为直径的⊙O交BC于点D,连接AD,请你添加一个条件,使△ABD≌△ACD,并说明全等的理由,你添加的条件是:BD=DC.
(1)如图,在△ABC中,以AB为直径的⊙O交BC于点D,连接AD,请你添加一个条件,使△ABD≌△ACD,并说明全等的理由,你添加的条件是:BD=DC.