题目内容
6.已知,下列关于x的一元二次方程(1)x2-1=0 (2)x2+x-2=0 (3)x2+2x-3=0 …(n)x2+(n-1)x-n=0
(1)求出方程(1)、方程(2)、方程(3)的根,并猜测方程(n)的根.
(2)请指出上述几个方程的根有什么共同特点,写出一条即可.
分析 (1)利用因式分解法分别求出方程(1)、方程(2)、方程(3)的根,根据以上3个方程的根,可猜测方程(n)的根;
(2)观察即可得出上述几个方程都有一个公共根是1.
解答 解:(1)(1)x2-1=0,
(x+1)(x-1)=0,
x+1=0,或x-1=0,
解得x1=-1,x2=1;
(2)x2+x-2=0,
(x+2)(x-1)=0,
x+2=0,或x-1=0,
解得x1=-2,x2=1;
(3)x2+2x-3=0,
(x+3)(x-1)=0,
x+3=0,或x-1=0,
解得x1=-3,x2=1;
…
猜测方程(n)x2+(n-1)x-n=0的根为x1=-n,x2=1;
(2)上述几个方程都有一个公共根是1.
点评 本题考查了一元二次方程的解(根)的意义:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.又因为只含有一个未知数的方程的解也叫做这个方程的根,所以,一元二次方程的解也称为一元二次方程的根.也考查了一元二次方程的解法.

练习册系列答案
相关题目
13.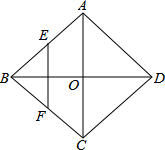 如图,菱形ABCD的对角线AC,BD相交于O点,E,F分别是AB,BC边上的中点,连接EF.若EF=$\sqrt{3}$,BD=4,则菱形ABCD的周长为( )
如图,菱形ABCD的对角线AC,BD相交于O点,E,F分别是AB,BC边上的中点,连接EF.若EF=$\sqrt{3}$,BD=4,则菱形ABCD的周长为( )
 如图,菱形ABCD的对角线AC,BD相交于O点,E,F分别是AB,BC边上的中点,连接EF.若EF=$\sqrt{3}$,BD=4,则菱形ABCD的周长为( )
如图,菱形ABCD的对角线AC,BD相交于O点,E,F分别是AB,BC边上的中点,连接EF.若EF=$\sqrt{3}$,BD=4,则菱形ABCD的周长为( )| A. | 4 | B. | 4$\sqrt{6}$ | C. | 4$\sqrt{7}$ | D. | 28 |
14.下列根式中,不能与$\sqrt{3}$合并的是( )
| A. | $\sqrt{\frac{1}{3}}$ | B. | $\frac{1}{\sqrt{3}}$ | C. | $\sqrt{\frac{2}{3}}$ | D. | $\sqrt{12}$ |
11.数学老师对黄华的8次单元考试成绩进行统计分析,要判断黄华的数学成绩是否稳定,老师需要知道黄华这8次数学成绩的( )
| A. | 平均数 | B. | 中位数 | C. | 众数 | D. | 方差 |
 如图,∠2=40°,∠3=100°,∠4=80°,求∠1的度数.
如图,∠2=40°,∠3=100°,∠4=80°,求∠1的度数.