题目内容
7.用配方法说明:不论x取何值,代数式2x2+5x-1的值总比代数式x2+7x-4的值大,并求出两代数式的差最小时x的值.分析 把两个代数式相减,进一步利用配方法证得2x2+5x-1-(x2+7x-4)>0,得出结论即可.
解答 解:2x2+5x-1-(x2+7x-4)
=2x2+5x-1-x2-7x+4
=x2-2x+3
=(x-1)2+2,
∵(x-1)2≥0,
∴(x-1)2+2>0
即2x2+5x-1-(x2+7x-4)>0,
∴不论x取任何值,代数式2x2+5y-1的值总比代数式x2+7x-4的值大,当x=1时,两代数式的差最小为2.
点评 此题考查利用作差法比较代数式的大小,以及配方法的运用;若证明一个代数式的值为非负数,需把这个代数式整理为一个完全平方式与一个正数的和的形式.

练习册系列答案
相关题目
5.轮船航行到C处观测小岛A的方向是南偏西54°,则从小岛A观测轮船在C处的方向是( )
| A. | 北偏东36° | B. | 北偏西36° | C. | 北偏东54° | D. | 北偏西54° |
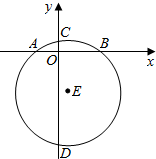 如图,在平面直角坐标系xOy中,直径为10的⊙E交x轴于点A、B,交y轴于点C、D,且点A、B的坐标分别为(-2,0)、(4,0).试求圆心E和点C、D的坐标.
如图,在平面直角坐标系xOy中,直径为10的⊙E交x轴于点A、B,交y轴于点C、D,且点A、B的坐标分别为(-2,0)、(4,0).试求圆心E和点C、D的坐标. 阅读材料,回答下列问题:
阅读材料,回答下列问题:
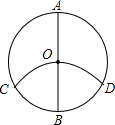 如图,AB为⊙O的直径,以点B为圆心,OB为半径作弧交⊙O与点C,D,求证:$\widehat{AC}$=$\widehat{AD}$=$\widehat{COD}$.
如图,AB为⊙O的直径,以点B为圆心,OB为半径作弧交⊙O与点C,D,求证:$\widehat{AC}$=$\widehat{AD}$=$\widehat{COD}$.