题目内容
7.如图,在△ABC中,∠B=2∠C,现有两个条件:①AD为△ABC的高;②AD为△ABC的角平分线.请从中选择一个条件,并解答下面的问题:(1)选择条件①.(填所选条件的序号)(下面两个图形供解题时选用)
(2)比较图中线段可以发现:AB+BD=CD(填图中的某一线段);证明你的结论.
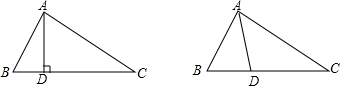
分析 选取条件①时,可以证明AB+BD=DC;在DC上截取DE=DB,连接EA,通过△ABD≌△AED,可得AB=AE;由角的关系可推得∠EAC=∠ECA可推得AE=EC,由CD=DE+CE,可得CD=AB+BD.
解答 解:若选①,AB+BD=DC;
证明:在DC上截取DE=DB,连接EA,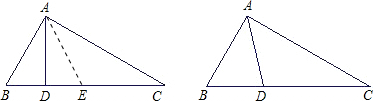
∵BD=ED,∠ADB=∠ADE=90°,AD为公共边,
∴△ABD≌△AED,
∴AB=AE,∠B=∠AED;
又∵∠B=2∠C,
∴∠AED=2∠C=∠C+∠EAC,
∴AE=EC,
即AB=AE=EC,
∵CD=DE+CE,
∴CD=AB+BD.
故答案为:①;CD.
点评 本题考查了全等三角形的判定和性质;解题时主要运用了比较线段的长短,涉及到全等三角形的判定及性质、等腰三角形的性质等知识点,是一道考查学生综合知识运用能力的好题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.下列说法中,正确的是( )
| A. | 一组邻边相等的四边形是菱形 | |
| B. | 对角线相等的平行四边形是菱形 | |
| C. | 对角线互相垂直的四边形是菱形 | |
| D. | 对角线交点到各边距离相等的四边形是菱形 |
17.用科学记数法记为4.01×104的原数是( )
| A. | 4010 | B. | 40100 | C. | 40.1 | D. | 401000 |
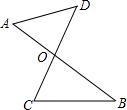 如图,线段AB、CD相交于点O,连接AD、CB.
如图,线段AB、CD相交于点O,连接AD、CB.