题目内容
4.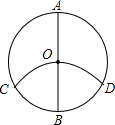 如图,AB为⊙O的直径,以点B为圆心,OB为半径作弧交⊙O与点C,D,求证:$\widehat{AC}$=$\widehat{AD}$=$\widehat{COD}$.
如图,AB为⊙O的直径,以点B为圆心,OB为半径作弧交⊙O与点C,D,求证:$\widehat{AC}$=$\widehat{AD}$=$\widehat{COD}$.
分析 连接AC、AD、BC、BD、CD、OC、OD,根据OB=OC=BC=BD=OD,证得△BOC和△BOD是等边三角形,四边形BCOD是菱形,从而证得∠COB=120°,AB垂直平分CD,进而证得△ACD是等边三角形,得出AC=AD=CD,根据圆心角、弧、弦的关系即可证得结论.
解答  证明:连接AC、AD、BC、BD、CD、OC、OD,
证明:连接AC、AD、BC、BD、CD、OC、OD,
∵OB=OC=BC=BD=OD,
∴△BOC和△BOD是等边三角形,四边形BCOD是菱形,
∴∠COB=120°,AB垂直平分CD,
∴∠CAD=60°,AC=AD,
∴△ACD是等边三角形,
∴AC=AD=CD,
∴$\widehat{AC}$=$\widehat{AD}$=$\widehat{COD}$.
点评 本题考查了圆心角、弧、弦的关系,等边三角形的判定和性质,菱形的判定和性质,作出辅助线构建等边三角形是解题的关键.

练习册系列答案
相关题目
12.下列说法中,正确的是( )
| A. | 一组邻边相等的四边形是菱形 | |
| B. | 对角线相等的平行四边形是菱形 | |
| C. | 对角线互相垂直的四边形是菱形 | |
| D. | 对角线交点到各边距离相等的四边形是菱形 |
14.甲、乙两名大学生竞选班长,现对甲、乙两名应聘者从笔试、口试、得票三个方面表现进行评分,各项成绩如表所示:
(1)如果按笔试占总成绩20%、口试占30%、得票占50%来计算各人的成绩,试判断谁会竞选上?
(2)如果将笔试、口试和得票按2:1:2来计算各人的成绩,那么又是谁会竞选上?
| 应聘者 | 笔试 | 口试 | 得票 |
| 甲 | 85 | 83 | 90 |
| 乙 | 80 | 85 | 92 |
(2)如果将笔试、口试和得票按2:1:2来计算各人的成绩,那么又是谁会竞选上?
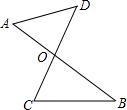 如图,线段AB、CD相交于点O,连接AD、CB.
如图,线段AB、CD相交于点O,连接AD、CB.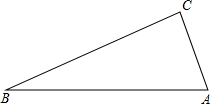 如图,△ABC中,AB=25,AC=7,BC=24,根据题中的已知,提出几个与△ABC有关的问题,并加以解决.
如图,△ABC中,AB=25,AC=7,BC=24,根据题中的已知,提出几个与△ABC有关的问题,并加以解决.