题目内容
9. 如图,在△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则B、D两点间的距离为$\sqrt{10}$.
如图,在△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则B、D两点间的距离为$\sqrt{10}$.
分析 由旋转的性质可求得AE、DE,由勾股定理可求得AB,则可求得BE,连接BD,在Rt△BDE中可求得BD的长.
解答  解:
解:
在△ABC中,∠C=90°,AC=4,BC=3,
∴AB=5,
∵△ABC绕点A逆时针旋转得到△AED,
∴∠DEA=∠C=90°,AE=AC=4,DE=BC=3,
∴BE=AB-AE=5-4=1,
连接BD,在Rt△BDE中,由勾股定理可得BD=$\sqrt{D{E}^{2}+B{E}^{2}}$=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,
即B、D两点间的距离为$\sqrt{10}$,
故答案为:$\sqrt{10}$.
点评 本题主要考查旋转的性质,掌握旋转前后对应线段相等、对应角相等是解题的关键.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
19. 如图,正六边形ABCDEF关于直线l的轴对称图形是六边形A′B′C′D′E′F′,下列判断错误的是( )
如图,正六边形ABCDEF关于直线l的轴对称图形是六边形A′B′C′D′E′F′,下列判断错误的是( )
 如图,正六边形ABCDEF关于直线l的轴对称图形是六边形A′B′C′D′E′F′,下列判断错误的是( )
如图,正六边形ABCDEF关于直线l的轴对称图形是六边形A′B′C′D′E′F′,下列判断错误的是( )| A. | 直线l⊥BB′ | B. | AB=A′B′ | C. | BC∥B′C′ | D. | BC∥A′B′ |
4.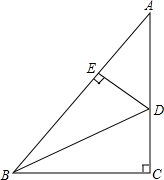 如图,Rt△ABC中,∠C=90°,BD是∠ABC的平分线,DE⊥AB于点E,AB=20cm,BC=12cm,△ABC的面积为96cm2,则DE的长是( )
如图,Rt△ABC中,∠C=90°,BD是∠ABC的平分线,DE⊥AB于点E,AB=20cm,BC=12cm,△ABC的面积为96cm2,则DE的长是( )
 如图,Rt△ABC中,∠C=90°,BD是∠ABC的平分线,DE⊥AB于点E,AB=20cm,BC=12cm,△ABC的面积为96cm2,则DE的长是( )
如图,Rt△ABC中,∠C=90°,BD是∠ABC的平分线,DE⊥AB于点E,AB=20cm,BC=12cm,△ABC的面积为96cm2,则DE的长是( )| A. | 4cm | B. | 6cm | C. | 8cm | D. | 10cm |
 如图,数轴上A点表示的数是a,B点表示的数是b,点A在点B的右边
如图,数轴上A点表示的数是a,B点表示的数是b,点A在点B的右边