题目内容
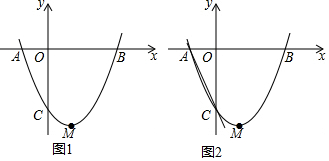
17.如图1,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-1,0),B(3,0)两点,与y轴交于点C(0,-3).(1)求该抛物线的解析式及顶点M的坐标;
(2)求△BCM的面积;
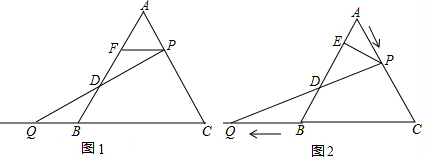
(3)若P是x轴上一个动点,过P作射线PQ∥AC交抛物线于点Q,随着P点的运动,在抛物线上是否存在这样的点Q,使以A、P、Q、C为顶点的四边形为平行四边形?若存在请求出Q点的坐标;若不存在,请说明理由.
分析 (1)A(-1,0),B(3,0),C(0,-3)代入y=ax 2+bx+c,解方程组即可.
(2)由抛物线y=x2-2x-3可知顶点M(1,-4).作MD⊥x轴于D,连结BC、CM、BM、OM.根据S△BCM=S△MOC+S△OBM-S△OBC计算即可.
(3)分两种情形讨论即可①当Q点在x轴下方时,作QE⊥x轴于E.②当Q1点在x轴上方时,作Q1F⊥x轴于F,分别求出点Q的纵坐标,转化为方程解决问题.
解答 解:(1)将A(-1,0),B(3,0),C(0,-3)代入y=ax 2+bx+c,
得到$\left\{\begin{array}{l}{a-b+c=0}\\{9a+3b+c=0}\\{c=-3}\end{array}\right.$
解得a=1,b=-2,c=-3;
∴y=x 2-2x-3.
(2)由抛物线y=x2-2x-3=(x-1)2-4,可知顶点M(1,-4).作MD⊥x轴于D,连结BC、CM、BM、OM.
∵S△BCM=S△MOC+S△OBM-S△OBC,
∴S△BCM=$\frac{1}{2}$×3×1+$\frac{1}{2}$×3×4-$\frac{1}{2}$×3×3=3.
(3)存在.
①当Q点在x轴下方时,作QE⊥x轴于E
∵AC∥PQ且AC=PQ∴OC=EQ=3
∴-3=x2-2x-3解得:x1=0(舍),x2=2
∴Q(2,-3)
②当Q1点在x轴上方时,作Q1F⊥x轴于F
∵AC∥P1Q1且AC=P1Q1
由Rt△OAC≌Rt△FP1Q1,
∴OC=FQ1=3
∴3=x2-2x-3解得:x=1$±\sqrt{7}$,
∴Q1坐标为(1+$\sqrt{7}$,3)或(1-$\sqrt{7}$,3),
综上,满足条件的Q点为(2,-3)或(1+$\sqrt{7}$,3)或(1-$\sqrt{7}$,3),
点评 本题考查二次函数综合题、三角形面积、平行线的性质.全等三角形的判定和性质等知识,解题的关键是灵活应用待定系数法确定函数解析式,学会利用分割法求三角形的面积,学会分类讨论的思想思考问题,属于中考压轴题.

 备战中考寒假系列答案
备战中考寒假系列答案| A. | (-2)-(-3) | B. | (-2)×(-3) | C. | (-2)2 | D. | (-3)3 |
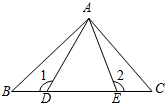 如图,AD=AE,BE=CD,∠1=∠2=130°,∠BAE=60°,则∠C的度数是( )
如图,AD=AE,BE=CD,∠1=∠2=130°,∠BAE=60°,则∠C的度数是( )| A. | 80° | B. | 70° | C. | 60° | D. | 50° |
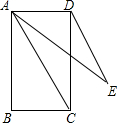 如图,矩形ABCD,AB=2$\sqrt{3}$,AC=4,将对角线AC绕点A旋转得到线段AE,连接DE,DE∥AC,则线段DE=-1+$\sqrt{13}$.
如图,矩形ABCD,AB=2$\sqrt{3}$,AC=4,将对角线AC绕点A旋转得到线段AE,连接DE,DE∥AC,则线段DE=-1+$\sqrt{13}$. 如图,在△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则B、D两点间的距离为$\sqrt{10}$.
如图,在△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则B、D两点间的距离为$\sqrt{10}$.