题目内容
18.不等式组$\left\{\begin{array}{l}{\frac{x-1}{2}≤3}\\{\frac{x+1}{3}>1}\end{array}\right.$的解集是2<x≤7.分析 先求出每个不等式的解集,再求出不等式组的解集即可.
解答 解:$\left\{\begin{array}{l}{\frac{x-1}{2}≤3①}\\{\frac{x+1}{3}>1②}\end{array}\right.$
∵由不等式①,x≤7;
由不等式②,得x>2,
∴原不等式组的解集是2<x≤7,
故答案为:2<x≤7.
点评 本题考查了解一元一次不等式组,能根据不等式的解集求出不等式组的解集是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.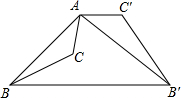 如图,已知钝角三角形ABC,将△ABC绕点A按逆时针方向旋转100°得到△AB′C′,连接BB′,若AC′∥BB′,则∠CAB′的度数为( )
如图,已知钝角三角形ABC,将△ABC绕点A按逆时针方向旋转100°得到△AB′C′,连接BB′,若AC′∥BB′,则∠CAB′的度数为( )
 如图,已知钝角三角形ABC,将△ABC绕点A按逆时针方向旋转100°得到△AB′C′,连接BB′,若AC′∥BB′,则∠CAB′的度数为( )
如图,已知钝角三角形ABC,将△ABC绕点A按逆时针方向旋转100°得到△AB′C′,连接BB′,若AC′∥BB′,则∠CAB′的度数为( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
10.某公司开发两种新产品,A型产品600件,B型产品400件,分配到甲、乙两地试销,其中甲地销售700件,乙地销售300件,两地销售这两种产品每件的利润(元)如表
设分配到甲地A型产品x件,公司售完这1000件产品的总利润为W(元)
(1)求W关于x的函数关系式,并求出最大利润是多少?
(2)为了加快A型产品的销售,公司决定对A型产品加强广告宣传,由于销售成本增加,A型产品的每件销售利润有所降低,甲地的每件销售利润降低$\frac{x}{100}$元,乙地的每件销售利润降低2元,那么公司售完这1000件产品最小可以获得多少利润?
| A型利润 | B型利润 | |
| 甲地 | 20 | 17 |
| 乙地 | 16 | 15 |
(1)求W关于x的函数关系式,并求出最大利润是多少?
(2)为了加快A型产品的销售,公司决定对A型产品加强广告宣传,由于销售成本增加,A型产品的每件销售利润有所降低,甲地的每件销售利润降低$\frac{x}{100}$元,乙地的每件销售利润降低2元,那么公司售完这1000件产品最小可以获得多少利润?
 四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF
四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF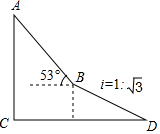 如图,为了测量出楼房AC的高度,从距离楼底C处60$\sqrt{3}$米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1:$\sqrt{3}$的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°=$\frac{4}{5}$,cos$\frac{3}{5}$=$\frac{3}{5}$,tan53°=$\frac{4}{3}$,$\sqrt{3}$≈1.732,结果精确到0.1米)
如图,为了测量出楼房AC的高度,从距离楼底C处60$\sqrt{3}$米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1:$\sqrt{3}$的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°=$\frac{4}{5}$,cos$\frac{3}{5}$=$\frac{3}{5}$,tan53°=$\frac{4}{3}$,$\sqrt{3}$≈1.732,结果精确到0.1米)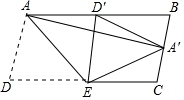 如图,将平行四边形纸片ABCD折叠,使得点D落在AB边上的D'处,折痕为AE.再将△AD'E翻折,点A恰好落在BC的中点A'处,连结AA',若AD=2,则线段AA'的长为$\sqrt{15}$.
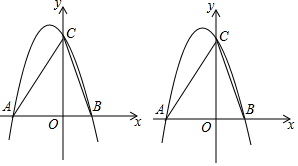
如图,将平行四边形纸片ABCD折叠,使得点D落在AB边上的D'处,折痕为AE.再将△AD'E翻折,点A恰好落在BC的中点A'处,连结AA',若AD=2,则线段AA'的长为$\sqrt{15}$.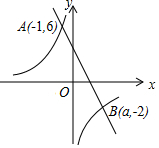 如图,在直角坐标系xoy中,一次函数y1=k1x+b的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象交于A(-1,6)、B(a,-2)两点.
如图,在直角坐标系xoy中,一次函数y1=k1x+b的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象交于A(-1,6)、B(a,-2)两点.