题目内容
6. 四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF
四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF(1)求证:△ADE≌△ABF;
(2)若BC=12,DE=4,求△AEF的面积.
分析 (1)根据SAS证明即可;
(2)首先证明△AEF是等腰三角形,求出AE的长即可解决问题;
解答 (1)证明:∵四边形ABCD是正方形,
∴AD=AB,∠D=∠ABC=90°,
而F是CB的延长线上的点,
∴∠ABF=90°,
在△ADE和△ABF中
$\left\{\begin{array}{l}{AD=AB}\\{∠D=∠ABF}\\{DE=BF}\end{array}\right.$,
∴△ADE≌△ABF(SAS);
(2)∵BC=12,
∴AD=12,
在Rt△ADE中,DE=4,AD=12,
∴AE=$\sqrt{A{D}^{2}+D{E}^{2}}$=4$\sqrt{10}$,
∵△ABF可以由△ADE绕旋转中心 A点,按顺时针方向旋转90度得到,
∴AE=AF,∠EAF=90°,
∴△AEF的面积=$\frac{1}{2}$AE2=$\frac{1}{2}$×160=80.
点评 本题考查正方形的性质、全等三角形的判定和性质、勾股定理、等腰三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
 如图,正方形网格中每个小正方形的边长均为1,线段AB的端点均在小正方形的顶点上.
如图,正方形网格中每个小正方形的边长均为1,线段AB的端点均在小正方形的顶点上.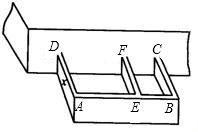 某农户计划利用现有的长为12米的一面墙再修四面墙,建造如图所示的长方体游泳池,培育不同品种的鱼苗,他已备足可以修高为2m,总长24m的墙的材料准备施工,设图中与现有一面墙垂直的三面墙的长度都为m,即AD=BF=BC=xm.(不考虑墙的厚度)
某农户计划利用现有的长为12米的一面墙再修四面墙,建造如图所示的长方体游泳池,培育不同品种的鱼苗,他已备足可以修高为2m,总长24m的墙的材料准备施工,设图中与现有一面墙垂直的三面墙的长度都为m,即AD=BF=BC=xm.(不考虑墙的厚度)