题目内容
(9分)某工厂生产的某种产品按质量分为10个档次,第一档次(最低档次)的产品一天可生产80件,每件产品的利润为10元,每提高一个档次,每件产品的利润增加2元.
(1)当每件产品的利润为16元时,此产品质量在第几档次?
(2)由于生产工序不同,此产品每提高一个档次,一天的产量减少4件.若生产某档次产品一天的总利润为1200元,问该工厂生产的是第几档次的产品?
(1)第四档次 (2)第六档次
【解析】
试题分析:(1)首先求出提高了几元钱,然后求出提高几个档次,然后进行说明;(2)设生产x档次的产品,则每件产品的利润为:10+2(x-1),产品的数量为:80-4(x-1),根据总利润=单件利润×数量列出方程进行计算.
试题解析:(1)当每件利润是16元时,提高了(16﹣10)÷2=3个档次,
∵提高3个档次 ∴此产品的质量档次是第4档次.
(2)设生产产品的质量档次是在第x档次时,一天的利润是y,
由题意可得y=[10+2(x﹣1)][80﹣4(x﹣1)],
整理得y=﹣8x2+136x+672,
当利润是1200元时,即﹣8x2+136x+672=1200,
解得:x1=6,x2=11(11>10,不符合题意,舍去)
答:当生产产品的质量档次是在第6档次时,一天的总利润为1200元.
考点:一元二次方程的应用.

练习册系列答案
相关题目
 经过点O,分别过A、B两点作AC⊥
经过点O,分别过A、B两点作AC⊥ 交
交
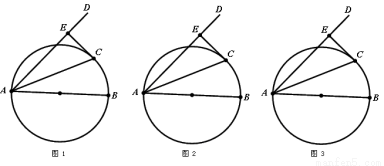


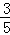 ,则BC的长是( )
,则BC的长是( )