题目内容
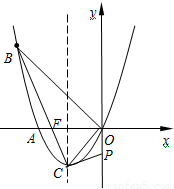
(11分)如图,已知抛物线经过A(﹣2,0),B(﹣3,3)及原点O,顶点为C.

(1)求抛物线的函数解析式.
(2)设点D在抛物线上,点E在抛物线的对称轴上,若四边形AODE是平行四边形,求点D的坐标.
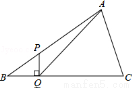
(3)联接BC交x轴于点F.y轴上是否存在点P,使得△POC与△BOF相似?若存在,求出点P的坐标;若不存在,请说明理由.
(1)y=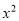 +2x;(2)D(1,3);(3)(0,-
+2x;(2)D(1,3);(3)(0,-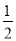 )或(0,-4)
)或(0,-4)
【解析】
试题分析:(1)将点A、点B和原点代入解析式进行求解;(2)根据平行四边形的性质得出点D的坐标;(3)首先求出OB、OF、OC的长度,然后根据三角形相似的条件求出点P的坐标,分两种情况进行讨论.
试题解析:(1)设抛物线的解析式为y=ax2+bx+c(a≠0),
将点A(﹣2,0),B(﹣3,3),O(0,0),代入可得: ,解得:
,解得: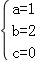 ,
,
所以函数解析式为:y=x2+2x;
(2)∵AO为平行四边形的一边, ∴DE∥AO,DE=AO, ∵A(﹣2,0),
∴DE=AO=2, ∵四边形AODE是平行四边形, ∴D在对称轴直线x=﹣1右侧,
∴D横坐标为:﹣1+2=1,代入抛物线解析式得y=3, ∴D的坐标为(1,3);
(3)在y轴上存在点P,使得△POC与△BOF相似,理由如下:
由y=x2+2x,顶点C的坐标为(﹣1,1) ∵tan∠BOF=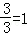 ,
,
∴∠BOF=45°, 当点P在y轴的负半轴时,tan∠COP=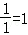 ,
,
∴∠COP=45°,∴∠BOF=∠COP, 设BC的解析式为y=kx+b(k≠0),
∵图象经过B(﹣3,3),C(﹣1,1)
∴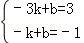 , 解得∴
, 解得∴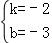 ,
,
∴y=﹣2x﹣3; 令y=0,则x=﹣1.5.
∴F(﹣1.5,0),
∴OB=3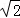 ,OF=1.5,OC=
,OF=1.5,OC=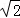 ,
,
①当△POC∽△FOB时, 则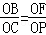 ,
,
即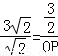 , ∴OP=
, ∴OP=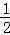 , ∴P(0,﹣
, ∴P(0,﹣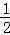 )
)
②当△POC∽△BOF时, ∴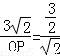 ,
,
∴OP=4, ∴P(0,﹣4),
∴当△POC与△BOF相似时,点P的坐标为(0,﹣ )或(0,﹣4).
)或(0,﹣4).
考点:待定系数法求函数解析式、三角形相似的判定、平行四边形的性质.


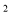 ,当小球达到最高点时,小球的运动时间为( )
,当小球达到最高点时,小球的运动时间为( )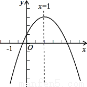
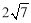 B.
B.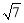 C.5 D.
C.5 D.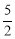
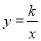 的图象与一次函数y=mx+b的图象交于A(1,3),B(n,-1)两点.
的图象与一次函数y=mx+b的图象交于A(1,3),B(n,-1)两点. 取何值时,反比例函数的值大于一次函数的值.
取何值时,反比例函数的值大于一次函数的值.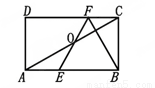
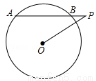
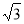 ,求AB的长。
,求AB的长。