题目内容
8.在RT△ABC中,∠C=90°,AB=10,sinA=$\frac{3}{5}$,那么AC=8.分析 首先由正弦函数的定义可知:$\frac{BC}{AB}$=$\frac{3}{5}$,从而可求得BC的长,然后由勾股定理可求得AC的长
解答  解:如图所示:
解:如图所示:
∵sin∠A=$\frac{BC}{AB}$=$\frac{3}{5}$,AB=10,
∴BC=6,
由勾股定理得:AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8.
故答案是:8.
点评 本题主要考查的是解直角三角形,掌握勾股定理和正弦函数的定义是解题的关键.

练习册系列答案
相关题目
16.若一个数的一个平方根是8,则这个数的立方根是( )
| A. | ±2 | B. | ±4 | C. | 2 | D. | 4 |
3.下列计算正确的是( )
| A. | (-2a2)3=-8a5 | B. | a3•a2=a5 | C. | 2a2+a2=3a4 | D. | (a-b)2=a2-b2 |
18.某校九年级(1)班的10名同学在“献爱心,关注留守儿童”捐款活动中,捐款情况如下(单位:元)10,8,12,15,10,12,11,9,10,13.关于这组数据,下列说法正确的是( )
| A. | 众数是10.5 | B. | 中位数是10 | C. | 平均数是11 | D. | 以上说法均不对 |
 为有效开发海洋资源,保护海洋权益,我国对南海诸岛进行了全面调查.如图,一测量船在A岛测得B岛在北偏西30°方向,C岛在北偏东15°方向,航行100海里到达B岛,在B岛测得C岛在北偏东45°,求B,C两岛及A,C两岛的距离.(结果保留到整数,$\sqrt{2}$≈1.41,$\sqrt{6}$≈2.45)
为有效开发海洋资源,保护海洋权益,我国对南海诸岛进行了全面调查.如图,一测量船在A岛测得B岛在北偏西30°方向,C岛在北偏东15°方向,航行100海里到达B岛,在B岛测得C岛在北偏东45°,求B,C两岛及A,C两岛的距离.(结果保留到整数,$\sqrt{2}$≈1.41,$\sqrt{6}$≈2.45)
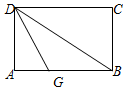 如图,将矩形纸片ABCD折叠,先折出折痕(对角线)BD,再折叠,使边DA与对角线BD重合,得折痕DG,若AB=8,BC=6,则AG的长是3.
如图,将矩形纸片ABCD折叠,先折出折痕(对角线)BD,再折叠,使边DA与对角线BD重合,得折痕DG,若AB=8,BC=6,则AG的长是3.