题目内容
19.有六张正面分别标有数字-2,-1,0,1,2,3 的不透明卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中任取一张,将该卡片上的数字记为a,将该卡片上的数字加-1记为-b.则数字a,b使得关于x的一元二次方程ax2+bx-1=0有解的概率为$\frac{5}{6}$.分析 根据题意可以求得a的取值范围,注意一元二次方程二次项系数不能为零,从而可以解答本题.
解答 解:由题意可得,
-b=a-1,则b=1-a,
∵关于x的一元二次方程ax2+bx-1=0有解,
∴b2-4a×(-1)=b2+4a=(1-a)2+4a≥0且a≠0,
解得,a为任意实数且a≠0,
∴数字a,b使得关于x的一元二次方程ax2+bx-1=0有解的概率为$\frac{5}{6}$,
故答案为:$\frac{5}{6}$.
点评 本题考查概率公式、根的判别式,解答本题的关键是明确题意,求出相应的概率,二次项系数忽略不能为零是易错点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.菱形两对角线长分别为24cm和10cm,则菱形的高为( ) cm.
| A. | 13 | B. | $\frac{240}{13}$ | C. | 120 | D. | $\frac{120}{13}$ |
14.已知方程mx2-2(1-m)x+m=0有实数根,则m满足的条件是( )
| A. | m≤$\frac{1}{2}$且m≠0 | B. | m<$\frac{1}{2}$且m≠0 | C. | m<$\frac{1}{2}$ | D. | m≤$\frac{1}{2}$ |
4.若a+b=-1,则2a+2b+1的值是( )
| A. | 0 | B. | -1 | C. | -2 | D. | -3 |
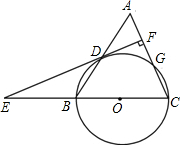 如图,等腰三角形ABC中,AC=BC=10,AB=12,以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E.
如图,等腰三角形ABC中,AC=BC=10,AB=12,以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E. 如图,将?ABCD沿对角线AC折叠,使点B落在B′处,若∠1=44°,∠D=120°,则∠2的度数为38°.
如图,将?ABCD沿对角线AC折叠,使点B落在B′处,若∠1=44°,∠D=120°,则∠2的度数为38°. 如图,已知线段AB=2,MN⊥AB于点M,且AM=BM,P是射线MN上一动点,E,D分别是PA,PB的中点,过点A,M,D的圆与BP的另一交点C(点C在线段BD上),连结AC,DE.
如图,已知线段AB=2,MN⊥AB于点M,且AM=BM,P是射线MN上一动点,E,D分别是PA,PB的中点,过点A,M,D的圆与BP的另一交点C(点C在线段BD上),连结AC,DE.