题目内容
6.用一个圆心角为120°,半径为18cm 的扇形作一个圆锥的侧面,则这个圆锥的底面半径应等于6cm.分析 设这个圆锥的底面半径为rcm,根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长和弧长公式得到2πr=$\frac{120×π×18}{180}$,然后解方程即可.
解答 解:设这个圆锥的底面半径为rcm,
根据题意得2πr=$\frac{120×π×18}{180}$,
解得r=6.
故答案为:6cm.
点评 本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
2.不等式组1≤x<2的解集在数轴上可表示为( )
| A. |  | B. |  | C. |  | D. |  |
14.函数y=$\frac{x-1}{x+2}$中x的取值范围为( )
| A. | x≠1 | B. | x≠-1 | C. | x≠-2 | D. | x≠2 |
15.若正比例函数的图象经过(-3,2),则这个图象一定经过点( )
| A. | (2,-3) | B. | $({\frac{3}{2},-1})$ | C. | (-1,1) | D. | (2,-2) |
16.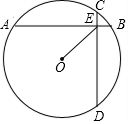 如图,在半径为6的⊙O内有两条互相垂直的弦AB和CD,AB=8,CD=6,垂足为E.则tan∠OEA的值是( )
如图,在半径为6的⊙O内有两条互相垂直的弦AB和CD,AB=8,CD=6,垂足为E.则tan∠OEA的值是( )
 如图,在半径为6的⊙O内有两条互相垂直的弦AB和CD,AB=8,CD=6,垂足为E.则tan∠OEA的值是( )
如图,在半径为6的⊙O内有两条互相垂直的弦AB和CD,AB=8,CD=6,垂足为E.则tan∠OEA的值是( )| A. | $\frac{3}{4}$ | B. | $\frac{\sqrt{6}}{3}$ | C. | $\frac{\sqrt{15}}{6}$ | D. | $\frac{2\sqrt{15}}{9}$ |
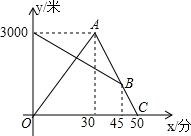 某天早晨,张强从家跑步去体育场锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,张强跑到体育场后发现要下雨,立即按原路返回,遇到妈妈后两人一起按他返回时的速度回到家(张强和妈妈始终在同一条笔直的公路上).设两人离家的距离为y(米),张强出发的时间为x(分),y与x之间的函数图象如图所示.
某天早晨,张强从家跑步去体育场锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,张强跑到体育场后发现要下雨,立即按原路返回,遇到妈妈后两人一起按他返回时的速度回到家(张强和妈妈始终在同一条笔直的公路上).设两人离家的距离为y(米),张强出发的时间为x(分),y与x之间的函数图象如图所示.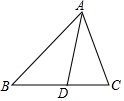 如图,在△ABC中,AD平分∠BAC交边BC于点D,BD=AD,AB=3,AC=2,那么AD的长是$\frac{3}{5}\sqrt{10}$.
如图,在△ABC中,AD平分∠BAC交边BC于点D,BD=AD,AB=3,AC=2,那么AD的长是$\frac{3}{5}\sqrt{10}$.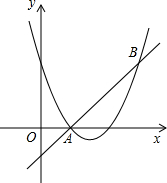 如图,直线y=x-1和抛物线y=x2+bx+c都经过点A(1,0),B(3,2).
如图,直线y=x-1和抛物线y=x2+bx+c都经过点A(1,0),B(3,2).