题目内容
15.四个角分别相等,四条边分别相等的两个四边形称为全等四边形.已知在四边形ABCD和四边形A′B′C′D′中,AB=A′B′,BC=B′C′,CD=C′D′.要使四边形ABCD≌四边形A′B′C′D′,可以添加的条件是( )| A. | DA=D′A′ | B. | ∠B=∠B′ | C. | ∠B=∠B′,∠C=∠C′ | D. | ∠B=∠B′,∠D=∠D′ |
分析 添加的条件是∠B=∠B′,∠C=∠C′,连接∠B=∠B′,∠C=∠C′,首先证明△ABC≌△A′B′C′可得∠ACB=∠A′C′B′,∠BAC=∠B′A′C′,然后再证明∴△ACD≌△A′C′D′可得AD=A′D′,∠DAC=∠D′A′C′,进而可得∠BAD=∠B′A′D′,然后可证明四边形ABCD≌四边形A′B′C′D′.
解答 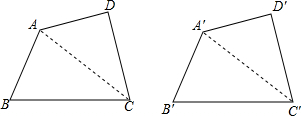 解:添加的条件是∠B=∠B′,∠C=∠C′,
解:添加的条件是∠B=∠B′,∠C=∠C′,
连接AC',A′C′,
∵在△ABC和△A′B′C′中$\left\{\begin{array}{l}{AB=A′B′}\\{∠B=∠B′}\\{CB=C′B′}\end{array}\right.$,
∴△ABC≌△A′B′C′(SAS),
∴∠ACB=∠A′C′B′,∠BAC=∠B′A′C′,AC=A′C′,
∵∠BCD=∠B′C′D′,
∴∠ACD=∠A′C′D′,
在△ACD和△A′C′D′中$\left\{\begin{array}{l}{AC=A′C′}\\{∠ACD=∠A′C′D′}\\{CD=C′D′}\end{array}\right.$,
∴△ACD≌△A′C′D′(SAS),
∴AD=A′D′,∠DAC=∠D′A′C′,
∴∠BAD=∠B′A′D′,
∴四边形ABCD≌四边形A′B′C′D′,
故答案选:C.
点评 此题主要考查了全等三角形的判定和性质,关键是掌握判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
3.已知反比例函数$y=\frac{k}{x}$(k<0)的图象上两点A(x1,y1)、B(x2,y2),且x1<x2<0,则下列不等式恒成立的是( )
| A. | y1•y2<0 | B. | y1+y2<0 | C. | y1-y2>0 | D. | y1-y2<0 |
20.化简|-2|的结果是( )
| A. | 一2 | B. | 2 | C. | $\frac{1}{2}$ | D. | ±2 |
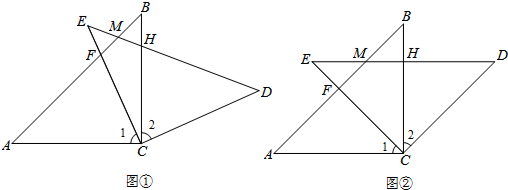
 如图,在Rt△ABC中,∠ACB=90°,AC=BC=9cm,动点P从点A出发,沿AB方向以每秒$\sqrt{2}$cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设Q点运动的时间为t秒,若四边形QP′CP为菱形,则t的值为3.
如图,在Rt△ABC中,∠ACB=90°,AC=BC=9cm,动点P从点A出发,沿AB方向以每秒$\sqrt{2}$cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设Q点运动的时间为t秒,若四边形QP′CP为菱形,则t的值为3.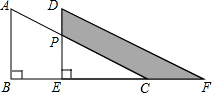 如图是重叠的两个直角三角形,将其中一个直角三角形沿BC方向平移得到△DEF.若AB=8,BE=6,DP=4,则图中阴影部分的面积为36cm2.
如图是重叠的两个直角三角形,将其中一个直角三角形沿BC方向平移得到△DEF.若AB=8,BE=6,DP=4,则图中阴影部分的面积为36cm2.