题目内容
12. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=9cm,动点P从点A出发,沿AB方向以每秒$\sqrt{2}$cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设Q点运动的时间为t秒,若四边形QP′CP为菱形,则t的值为3.
如图,在Rt△ABC中,∠ACB=90°,AC=BC=9cm,动点P从点A出发,沿AB方向以每秒$\sqrt{2}$cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设Q点运动的时间为t秒,若四边形QP′CP为菱形,则t的值为3.
分析 连接PP′交BC于O,如图,利用等腰直角三角形的性质得AB=$\sqrt{2}$AC=9$\sqrt{2}$,由于BQ=t,PA=$\sqrt{2}$t,则PB=9$\sqrt{2}$-$\sqrt{2}$t,CQ=9-t,根据菱形的性质得PP′⊥QC,OQ=OC,则OQ=$\frac{9-t}{2}$,BO=$\frac{9+t}{2}$,然后利用PO∥AC,得到$\frac{BO}{BC}$=$\frac{BP}{BA}$,即$\frac{\frac{9+t}{2}}{9}$=$\frac{9\sqrt{2}-\sqrt{2}t}{9\sqrt{2}}$,再利用比例性质求t即可.
解答 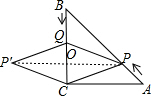 解:连接PP′交BC于O,如图,∵∠ACB=90°,AC=BC=9cm,
解:连接PP′交BC于O,如图,∵∠ACB=90°,AC=BC=9cm,
∴AB=$\sqrt{2}$AC=9$\sqrt{2}$,
∵BQ=t,PA=$\sqrt{2}$t,
∴PB=9$\sqrt{2}$-$\sqrt{2}$t,CQ=9-t,
∵若四边形QPCP′为菱形,
∴PP′⊥QC,OQ=OC
∴OQ=$\frac{9-t}{2}$,
∴BO=t+$\frac{9-t}{2}$=$\frac{9+t}{2}$
∵∠POQ=90°,∠ACB=90°,
∴PO∥AC,
∴$\frac{BO}{BC}$=$\frac{BP}{BA}$,即$\frac{\frac{9+t}{2}}{9}$=$\frac{9\sqrt{2}-\sqrt{2}t}{9\sqrt{2}}$,
∴t=3.
故答案为3.
点评 本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了菱形的性质和平行线分线段成比例定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.四个角分别相等,四条边分别相等的两个四边形称为全等四边形.已知在四边形ABCD和四边形A′B′C′D′中,AB=A′B′,BC=B′C′,CD=C′D′.要使四边形ABCD≌四边形A′B′C′D′,可以添加的条件是( )
| A. | DA=D′A′ | B. | ∠B=∠B′ | C. | ∠B=∠B′,∠C=∠C′ | D. | ∠B=∠B′,∠D=∠D′ |
7.某服装经销商甲.库存有进价每套400元的A品牌服装1200套,正常销售时每套600元,每月可卖出100套,一年内刚好卖完,现在市场上流行B品牌服装,此品牌服装进价每套200元,售出价每套500元,每月可卖出120套(两种服装的市场行情互不受影响),目前有一可进B品牌服装的机会,若这一机会错过,估计一年内进不到这种服装.可是,经销商甲手头无流动资金可用,只有低价转让A品牌服装,经与经销商乙协商,达成协议,转让价格(元/套)与转让数量(套)有如下关系:
(1)猜想并求出转让价格与转让数量之间的函数关系;
(2)现在经销商甲面临三种选择:
方案1:不转让A品牌服装,也不经销B品牌服装;
方案2:全部转让A品牌服装,用转让来的资金购B品牌服装,经销B品牌服装;
方案3:部分转让A品牌服装,用转让来的资金购B品牌服装,经销B品牌服装,同时也经销A品牌服装.
如果你是经销商甲,为使自己在服装经销过程中获得最大利润,你选择哪一种方案?怎样选择?为什么?
| 转让数量(套) | 1200 | 1100 | 1000 | 900 | 800 | 700 | 600 | 500 | 400 | 300 | 200 | 100 |
| 价格(元/套) | 240 | 250 | 260 | 270 | 280 | 290 | 300 | 310 | 320 | 330 | 340 | 350 |
(2)现在经销商甲面临三种选择:
方案1:不转让A品牌服装,也不经销B品牌服装;
方案2:全部转让A品牌服装,用转让来的资金购B品牌服装,经销B品牌服装;
方案3:部分转让A品牌服装,用转让来的资金购B品牌服装,经销B品牌服装,同时也经销A品牌服装.
如果你是经销商甲,为使自己在服装经销过程中获得最大利润,你选择哪一种方案?怎样选择?为什么?
2.下面各组函数中为相同函数的是( )
| A. | f(x)=$\sqrt{(x-1)^{2}}$,g(x)=x-1 | B. | f(x)=$\sqrt{{x}^{2}-1}$,g(x)=$\sqrt{x+1}$$\sqrt{x-1}$ | ||
| C. | f(x)=($\sqrt{x-1}$)2,g(x)=$\sqrt{(x-1)^{2}}$ | D. | f(x)=$\sqrt{\frac{{x}^{2}-1}{x+2}}$,g(x)=$\frac{\sqrt{{x}^{2}-1}}{\sqrt{x+2}}$ |
 在Rt△ABC中,∠C=90°.
在Rt△ABC中,∠C=90°.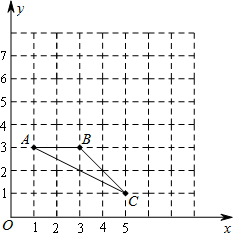 已知△ABC在平面直角坐标系中的位置如图所示.画出△ABC绕点A逆时针旋转90°后的△AB′C′,并写出点B,C的对应点B′,C′的坐标.
已知△ABC在平面直角坐标系中的位置如图所示.画出△ABC绕点A逆时针旋转90°后的△AB′C′,并写出点B,C的对应点B′,C′的坐标.