题目内容
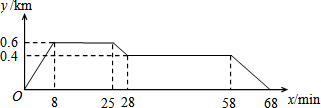
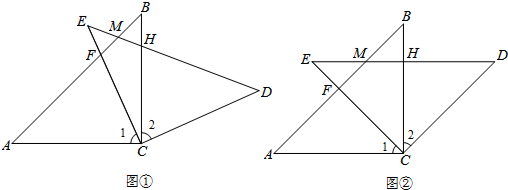
10.如图①,在Rt△ABC和Rt△EDC中,∠ACB=∠ECD=90°,AC=EC=BC=DC,AB与EC交于F,ED与AB、BC分别交于M、H.(1)求证:CF=CH;
(2)如图②,Rt△ABC不动,将Rt△EDC绕点C旋转到∠BCE=45°时,判断四边形ACDM的形状,并证明你的结论.
分析 (1)求出∠1=∠2,∠A=∠B=∠D=∠E=45°,根据ASA推出△ACF≌△DCH,根据全等三角形的性质得出即可;
(2)求出四边形ACDM是平行四边形,根据菱形的判定得出即可.
解答 (1)证明:∵∠ACB=∠ECD=90°,AC=BC=CD=CE,
∴∠1=∠2=90°-∠BCE,∠A=∠B=∠D=∠E=45°,
在△ACF和△DCH中
$\left\{\begin{array}{l}{∠A=∠D}\\{AC=CD}\\{∠1=∠2}\end{array}\right.$
∴△ACF≌△DCH,
∴CF=CH;
(2)四边形ACDM是菱形,
证明:∵∠ACB=∠ECD=90°,∠BCE=45°,
∴∠1=∠2=90°-45°=45°,
∵∠A=∠D=45°,
∴∠A+∠ACD=45°+90°+45°=180°,
同理∠D+∠ACD=180°,
∴AM∥DC,AC∥DM,
∴四边形ACDM是平行四边形,
∵AC=CD,
∴四边形ACDM是菱形.
点评 本题考查了等腰三角形的性质,平行线的判定,全等三角形的判定和性质的应用,能求出△ACF≌△DCH和四边形ACDM是平行四边形是解此题的关键,综合性比较强.

练习册系列答案
相关题目
15.四个角分别相等,四条边分别相等的两个四边形称为全等四边形.已知在四边形ABCD和四边形A′B′C′D′中,AB=A′B′,BC=B′C′,CD=C′D′.要使四边形ABCD≌四边形A′B′C′D′,可以添加的条件是( )
| A. | DA=D′A′ | B. | ∠B=∠B′ | C. | ∠B=∠B′,∠C=∠C′ | D. | ∠B=∠B′,∠D=∠D′ |
2.下列运算正确的是( )
| A. | x3+x3=2x6 | B. | (-x5)4=x20 | C. | xm•xn=xmn | D. | x8÷x2=x4 |
7.某服装经销商甲.库存有进价每套400元的A品牌服装1200套,正常销售时每套600元,每月可卖出100套,一年内刚好卖完,现在市场上流行B品牌服装,此品牌服装进价每套200元,售出价每套500元,每月可卖出120套(两种服装的市场行情互不受影响),目前有一可进B品牌服装的机会,若这一机会错过,估计一年内进不到这种服装.可是,经销商甲手头无流动资金可用,只有低价转让A品牌服装,经与经销商乙协商,达成协议,转让价格(元/套)与转让数量(套)有如下关系:
(1)猜想并求出转让价格与转让数量之间的函数关系;
(2)现在经销商甲面临三种选择:
方案1:不转让A品牌服装,也不经销B品牌服装;
方案2:全部转让A品牌服装,用转让来的资金购B品牌服装,经销B品牌服装;
方案3:部分转让A品牌服装,用转让来的资金购B品牌服装,经销B品牌服装,同时也经销A品牌服装.
如果你是经销商甲,为使自己在服装经销过程中获得最大利润,你选择哪一种方案?怎样选择?为什么?
| 转让数量(套) | 1200 | 1100 | 1000 | 900 | 800 | 700 | 600 | 500 | 400 | 300 | 200 | 100 |
| 价格(元/套) | 240 | 250 | 260 | 270 | 280 | 290 | 300 | 310 | 320 | 330 | 340 | 350 |
(2)现在经销商甲面临三种选择:
方案1:不转让A品牌服装,也不经销B品牌服装;
方案2:全部转让A品牌服装,用转让来的资金购B品牌服装,经销B品牌服装;
方案3:部分转让A品牌服装,用转让来的资金购B品牌服装,经销B品牌服装,同时也经销A品牌服装.
如果你是经销商甲,为使自己在服装经销过程中获得最大利润,你选择哪一种方案?怎样选择?为什么?