题目内容
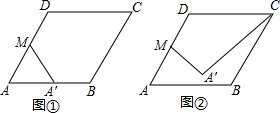
2. 如图,△ABC中,BD是角平分线,过D作DE∥AB交BC于点E,AB=5cm,BE=3cm,分别求出DE与EC的长.
如图,△ABC中,BD是角平分线,过D作DE∥AB交BC于点E,AB=5cm,BE=3cm,分别求出DE与EC的长.
分析 先利用角平分线定义和平行线性质得到∠ABD=∠CBD,∠ABD=∠BDE,则∠BDE=∠EBD,于是根据等腰三角形的性质得DE=BE=3cm,再根据平行于三角形的一边,并且和其他两边(或两边的延长线)相交的直线,所截得的三角形的三边与原三角形的三边对应成比例得到∴$\frac{DE}{AB}$=$\frac{CE}{CB}$,即$\frac{3}{5}$=$\frac{CE}{CE+3}$,然后利用比例性质计算CE.
解答 解:∵BD是角平分线,
∴∠ABD=∠CBD,
∵DE∥AB,
∴∠ABD=∠BDE,
∴∠BDE=∠EBD,
∴DE=BE=3cm,
∵DE∥AB,
∴$\frac{DE}{AB}$=$\frac{CE}{CB}$,即$\frac{3}{5}$=$\frac{CE}{CE+3}$,解得CE=$\frac{9}{2}$(cm).
答:DE与EC的长分别为3cm、$\frac{9}{2}$cm.
点评 本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例;平行于三角形的一边,并且和其他两边(或两边的延长线)相交的直线,所截得的三角形的三边与原三角形的三边对应成比例.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
17.下列语句中正确的是( )
| A. | 相等的圆心角所对的弧相等 | B. | 三点确定一个圆 | ||
| C. | 长度相等的弧是等弧 | D. | 矩形的四个顶点在同一个圆上 |
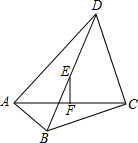 已知:如图,在四边形ABCD中,∠BAD=∠BCD=90°,E,F分别是对角线BD,AC的中点.求证:EF⊥AC.
已知:如图,在四边形ABCD中,∠BAD=∠BCD=90°,E,F分别是对角线BD,AC的中点.求证:EF⊥AC.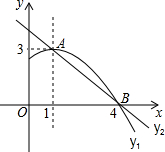 如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:
如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论: