题目内容
12.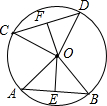 如图,在⊙O中,AB与CD是两条弦,OE⊥AB,OF⊥CD,垂足分别是点E,F,OE,OF分别叫做弦AB,CD的弦心距.
如图,在⊙O中,AB与CD是两条弦,OE⊥AB,OF⊥CD,垂足分别是点E,F,OE,OF分别叫做弦AB,CD的弦心距.(1)已知∠AOB=∠COD,求证:OE=OF;
(2)已知OE=OF,求证:AB=CD,$\widehat{AB}$=$\widehat{CD}$,∠AOB=∠COD;
(3)你能用文字语言把上述结论表述出来吗?
分析 (1)求出∠OEB=∠OFD=90°,∠EOB=∠FOD,证△EOB≌△FOD,即可推出OE=OF.
(2)证△EOB≌△FOD,推出BE=DF,根据垂径定理求出AB=CD,根据圆心角、弧、弦之间的关系即可得出答案.
(3)根据(1)(2)用文字语言把上述结论表述出来即可.
解答 (1)证明:∵OE⊥AB,OF⊥CD,OA=OB,OC=OD,
∴∠OEB=∠OFD=90°,∠EOB=$\frac{1}{2}$∠AOB,∠FOD=$\frac{1}{2}$∠COD,
∵∠AOB=∠COD,
∴∠EOB=∠FOD,
∵在△EOB和△FOD中,
$\left\{\begin{array}{l}{∠OEB=∠OFD}\\{∠EOB=∠FOD}\\{OB=OD}\end{array}\right.$
∴△EOB≌△FOD(AAS),
∴OE=OF.
(2)证明:∵OE⊥AB,OF⊥CD,
∴∠OEB=∠OFD=90°,
∵在Rt△BEO和Rt△DFO中,
$\left\{\begin{array}{l}{OB=OD}\\{OE=OF}\end{array}\right.$
∴Rt△BEO≌Rt△DFO(HL),
∴BE=DF,
由垂径定理得:AB=2BE,CD=2DF,
∴AB=CD,
∴$\widehat{AB}$=$\widehat{CD}$,∠AOB=∠COD.
(3)在同圆或等圆中,相等的圆心角所对应的弦心距相等;反过来,在同圆或等圆中,弦心距相等,所对应的圆心角相等,所对应的弦相等,所对应的弧相等.
点评 本题考查了全等三角形性质和判定,等腰三角形的性质和判定,垂径定理,圆心角、弧、弦之间的关系等知识点的应用,主要考查学生运用定理进行推理的能力.

练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
2.在3×3的方阵图中,填写了一些数和代数式(其中每个代数式表示一个数)使得每行的3个数,每列的3个数,斜对角的3个数之和均相等.
(1)求x、y的值;
(2)将方阵中的空格部分填上正确的数.
(1)求x、y的值;
(2)将方阵中的空格部分填上正确的数.
| 6 | 1 | 2x-4 |
| y-x | 3y-x | 7 |
| 4 | 5 | 0 |
17.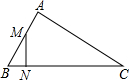 如图,△ABC中,M是AB的中点,N在BC上,BC=2AB,∠BMN=∠C,则△BMN∽△BCA,相似比为$\frac{1}{4}$,$\frac{BN}{NC}$=$\frac{1}{7}$.
如图,△ABC中,M是AB的中点,N在BC上,BC=2AB,∠BMN=∠C,则△BMN∽△BCA,相似比为$\frac{1}{4}$,$\frac{BN}{NC}$=$\frac{1}{7}$.
 如图,△ABC中,M是AB的中点,N在BC上,BC=2AB,∠BMN=∠C,则△BMN∽△BCA,相似比为$\frac{1}{4}$,$\frac{BN}{NC}$=$\frac{1}{7}$.
如图,△ABC中,M是AB的中点,N在BC上,BC=2AB,∠BMN=∠C,则△BMN∽△BCA,相似比为$\frac{1}{4}$,$\frac{BN}{NC}$=$\frac{1}{7}$. 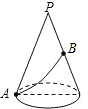 如图,一个圆锥的母线长为10cm,底面半径为5cm,在圆锥的底面边缘上一点A处有一只蚂蚁,想吃到点A相对的母线的中点B处的一粒砂糖,这只蚂蚁从点A出发,沿着曲面爬到点B,最短路线的长是多少?
如图,一个圆锥的母线长为10cm,底面半径为5cm,在圆锥的底面边缘上一点A处有一只蚂蚁,想吃到点A相对的母线的中点B处的一粒砂糖,这只蚂蚁从点A出发,沿着曲面爬到点B,最短路线的长是多少? 如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“→”方向排序,如(1,0),(2,0)(2,1),(1,1)(1,2)(2,2),…,根据这个规律,第2015个点的横坐标为( )
如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“→”方向排序,如(1,0),(2,0)(2,1),(1,1)(1,2)(2,2),…,根据这个规律,第2015个点的横坐标为( )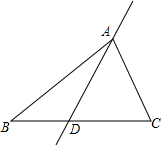 如图,已知△ABC,点D在BC边上,过点A作直线AD.
如图,已知△ABC,点D在BC边上,过点A作直线AD.