题目内容
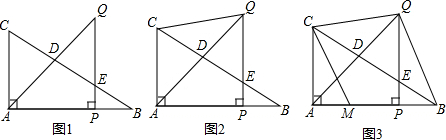
4. 如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“→”方向排序,如(1,0),(2,0)(2,1),(1,1)(1,2)(2,2),…,根据这个规律,第2015个点的横坐标为( )
如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“→”方向排序,如(1,0),(2,0)(2,1),(1,1)(1,2)(2,2),…,根据这个规律,第2015个点的横坐标为( )| A. | 44 | B. | 45 | C. | 46 | D. | 47 |
分析 根据图形,观察不难发现,点的个数按照平方数的规律变化,并且横坐标是奇数时,纵坐标逐渐变小,横坐标是偶数时,纵坐标逐渐变大,然后求出与2015最接近的平方数,求解即可.
解答  解:∵452=2025,
解:∵452=2025,
∴第2025个点的横坐标为45,
∵2025-2015=10,
∴第2015个点在第2025个点的正上方10个单位处,
∴第2015个点的坐标为(45,10).
故选B.
点评 本题考查了点的坐标的规律变化,利用与2015最接近的完全平方数个点的坐标求解是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.若x-3y=-5,则代数式5-2x+6y的值是( )
| A. | 0 | B. | 5 | C. | 10 | D. | 15 |
14.某电器按成本价提高30%后标价,再打八折销售,售价为2080元.设该电器的成本价为x元,由题意,下面所列方程正确的是( )
| A. | 80%(1+30%)x=2080 | B. | 30%•80%x=2080 | C. | 2080×30%×80%=x | D. | 30%•x=2080×80% |
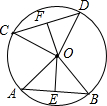 如图,在⊙O中,AB与CD是两条弦,OE⊥AB,OF⊥CD,垂足分别是点E,F,OE,OF分别叫做弦AB,CD的弦心距.
如图,在⊙O中,AB与CD是两条弦,OE⊥AB,OF⊥CD,垂足分别是点E,F,OE,OF分别叫做弦AB,CD的弦心距.
 如图,圆锥的高SO=4cm,底面圆的直径AB=6cm,求圆锥的侧面积.
如图,圆锥的高SO=4cm,底面圆的直径AB=6cm,求圆锥的侧面积.