题目内容
19. 已知:如图,DE∥BC,BE平分∠ABC.求证:∠1=∠3.
已知:如图,DE∥BC,BE平分∠ABC.求证:∠1=∠3.
分析 根据平行线的性质求出∠2=∠3,根据角平分线定义求出∠1=∠2,即可得出答案.
解答 证明:∵DE∥BC,
∴∠2=∠3,
∵BE平分∠ABC,
∴∠1=∠2,
∴∠1=∠3.
点评 本题考查了角平分线定义,平行线的性质的应用,能求出∠1=∠2,∠2=∠3是解此题的关键,注意:两直线平行,同位角相等.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
9.在△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边,下列式子一定能成立的是( )
| A. | a=csinB | B. | a=bcosB | C. | c=atanB | D. | a=btanA |
7.顺次连接对角线相等的各边中点所得的四边形一定是( )
| A. | 菱形 | B. | 正方形 | C. | 平行四边形 | D. | 矩形 |
4.Rt△ABC中,∠ACB=90°,若∠ACD=50°,则与∠BCD相邻的外角度数是( )
| A. | 130° | B. | 140° | C. | 40° | D. | 40°或140° |
9.设△ABC的三边长分别为a、b、c,其外接圆半径为R,若R=$\frac{a\sqrt{bc}}{b+c}$,则△ABC的最大角是( )
| A. | 75° | B. | 120° | C. | 90° | D. | 150° |
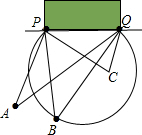 如图,在“世界杯”足球比赛中,甲带球向对方球门PQ进攻,当他带球冲到A点时,同样乙已经助攻冲到B点,丙助攻到C点.有三种射门方式:第一种是甲直接射门;第二种是甲将球传给乙,由乙射门.第三种是甲将球传给丙,由丙射门.仅从射门角度考虑,应选择第三种射门方式.
如图,在“世界杯”足球比赛中,甲带球向对方球门PQ进攻,当他带球冲到A点时,同样乙已经助攻冲到B点,丙助攻到C点.有三种射门方式:第一种是甲直接射门;第二种是甲将球传给乙,由乙射门.第三种是甲将球传给丙,由丙射门.仅从射门角度考虑,应选择第三种射门方式. 分别作出△ABC关于OD、OE对称的三角形.
分别作出△ABC关于OD、OE对称的三角形.