题目内容
11.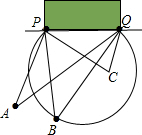 如图,在“世界杯”足球比赛中,甲带球向对方球门PQ进攻,当他带球冲到A点时,同样乙已经助攻冲到B点,丙助攻到C点.有三种射门方式:第一种是甲直接射门;第二种是甲将球传给乙,由乙射门.第三种是甲将球传给丙,由丙射门.仅从射门角度考虑,应选择第三种射门方式.
如图,在“世界杯”足球比赛中,甲带球向对方球门PQ进攻,当他带球冲到A点时,同样乙已经助攻冲到B点,丙助攻到C点.有三种射门方式:第一种是甲直接射门;第二种是甲将球传给乙,由乙射门.第三种是甲将球传给丙,由丙射门.仅从射门角度考虑,应选择第三种射门方式.
分析 本题实际是求∠A和∠B以及∠C度数的大小;可设AP与⊙O的交点为C′,连接QC′,由圆周角定理可得∠PC′Q=∠B;由于∠PC′Q是△APQ的外角,显然∠PC′Q即∠B的度数要大于∠A;因此从射门角度考虑,在B点射门时,射门的角度更大,更有利于进球,又因为圆内角大于圆外角,所以∠C>∠B,进而可得第三种射门方式最佳.
解答 解:设AP与圆的交点是C,连接CQ;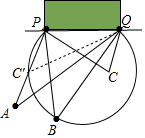
则∠PCQ>∠A;
由圆周角定理知:∠PCQ=∠B;
所以∠B>∠A;
因为∠C>∠B,
因此选择第种射三门方式更好.
故答案为:第三.
点评 此题实际上是比较两个角的大小,角度越大,射中率越高.综合考查了圆周角定理和三角形外角的性质.

练习册系列答案
相关题目
1.下列各式中,能用平方差公式计算的是( )
| A. | (3m-5)(5-3m) | B. | (2x+y)(y-2x) | ||
| C. | (2a2+3abc)(-2a2-3abc) | D. | (4b-2b)(3a+2b) |
1.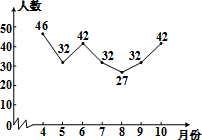 小红根据去年4~10月本班同学去孔学堂听中国传统文化讲座的人数,绘制了如图所示的折线统计图,图中统计数据的众数是( )
小红根据去年4~10月本班同学去孔学堂听中国传统文化讲座的人数,绘制了如图所示的折线统计图,图中统计数据的众数是( )
 小红根据去年4~10月本班同学去孔学堂听中国传统文化讲座的人数,绘制了如图所示的折线统计图,图中统计数据的众数是( )
小红根据去年4~10月本班同学去孔学堂听中国传统文化讲座的人数,绘制了如图所示的折线统计图,图中统计数据的众数是( )| A. | 46 | B. | 42 | C. | 32 | D. | 27 |
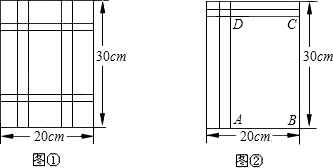
 已知:如图,DE∥BC,BE平分∠ABC.求证:∠1=∠3.
已知:如图,DE∥BC,BE平分∠ABC.求证:∠1=∠3.