题目内容
14.某商场超市经销一种销售成本为每千克40元的水产品,据市场分析,若按每千克50元销售,一个月能售出500kg;销售单价每涨1元,月销售量就减少10kg,设销售单价为每千克x元,月销售利润为y元.(1)求y与x之间的函数关系式;
(2)画出(1)中函数图象(不考虑x取值范围);
(3)观察图象,x取何值时,y=0;当x在什么范围变化时,经销这种水产品不亏本.
(4)超市想在月销售成本不超过10000元的情况下,使得月销售利润达到8000元,销售单价应定为多少?
分析 (1)月销售利润=每千克的利润×可卖出千克数,把相关数值代入即可;
(2)求出二次函数与x轴的交点坐标以及顶点坐标画出函数图象即可;
(3)根据图象数形结合回答问题;
(4)根据(1)中利润y与x之间的函数关系式,然后令y=8000,解出x,进行检验即可.
解答 解:(1)可卖出千克数为500-10(x-50)=1000-10x,
y与x的函数表达式为y=(x-40)(1000-10x)=-10x2+1400x-40000;
(2)y=-10x2+1400x-40000与x轴的交点坐标为(40,0)(100,0);顶点坐标为(70,9000)
函数图象如下: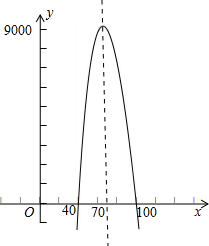
(3)观察图象可知,x=40或100时,y=0;
当40≤x≤100时,经销这种水产品不亏本;
(4)y=(x-40)×(1000-10x),
令y=8000,解得x1=60,x2=80.
当x1=60时,销售价为60元,月销售量为400千克,则成本价为40×400=16000(元),超过了10000元,不合题意,舍去;
当x2=80时,销售价为80元,月销售量为200千克,则成本价为40×200=8000(元),低于10000元,符合题意.
故销售价为80元.
点评 本题主要考查了二次函数的图象和性质,首先读懂题意,找到合适的等量关系,然后正确列出函数表达式和方程是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.在平面直角坐标系中,将点A(1,2)的横坐标乘以-1,纵坐标乘以-1,得到点A′,则点A与点A′的关系是( )
| A. | 关于x轴对称 | |
| B. | 关于y轴对称 | |
| C. | 关于原点对称 | |
| D. | 将点A向x轴负方向平移一个单位得点A |
 已知:如图,DE∥BC,BE平分∠ABC.求证:∠1=∠3.
已知:如图,DE∥BC,BE平分∠ABC.求证:∠1=∠3.