题目内容
已知函数y=ax2+5x-2,根据下列条件求a的取值范围:
(1)函数图象与x轴有两个交点;
(2)函数图象与x轴有交点;
(3)函数图象与x轴没有交点;
(4)函数值能够恒为负数吗?能够恒为正数吗?说明理由.
(1)函数图象与x轴有两个交点;
(2)函数图象与x轴有交点;
(3)函数图象与x轴没有交点;
(4)函数值能够恒为负数吗?能够恒为正数吗?说明理由.
考点:抛物线与x轴的交点
专题:
分析:令y=0,则ax2+5x-2=0,根据二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的交点与一元二次方程ax2+bx+c=0根之间的关系即可判断a的取值;
解答:解(1)∵函数图象与x轴有两个交点,则b2-4ac>0,
∴52-4a×(-2)>0,
解得:a>-
;
(2)∵函数图象与x轴有交点,则b2-4ac≥0,
∴52-4a×(-2)≥0,
解得:a≥-
;
(3)∵函数图象与x轴没有交点,则b2-4ac<0,
∴52-4a×(-2)<0,
解得:a<-
;
(4)能;
当a>0,抛物线的开口向上,如果函数的图象与x轴没有交点,则函数值恒为正数,
当a<0,抛物线的开口向下,如果函数的图象与x轴没有交点,则函数值恒为负数.
∴52-4a×(-2)>0,
解得:a>-
| 25 |
| 8 |
(2)∵函数图象与x轴有交点,则b2-4ac≥0,
∴52-4a×(-2)≥0,
解得:a≥-
| 25 |
| 8 |
(3)∵函数图象与x轴没有交点,则b2-4ac<0,
∴52-4a×(-2)<0,
解得:a<-
| 25 |
| 8 |
(4)能;
当a>0,抛物线的开口向上,如果函数的图象与x轴没有交点,则函数值恒为正数,
当a<0,抛物线的开口向下,如果函数的图象与x轴没有交点,则函数值恒为负数.
点评:本题考查了抛物线与x轴的交点.二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的交点与一元二次方程ax2+bx+c=0根之间的关系.
△=b2-4ac决定抛物线与x轴的交点个数.
△=b2-4ac>0时,抛物线与x轴有2个交点;
△=b2-4ac=0时,抛物线与x轴有1个交点;
△=b2-4ac<0时,抛物线与x轴没有交点.
△=b2-4ac决定抛物线与x轴的交点个数.
△=b2-4ac>0时,抛物线与x轴有2个交点;
△=b2-4ac=0时,抛物线与x轴有1个交点;
△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
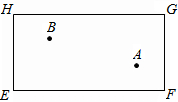 如图,四边形EFGH为长方形的台球桌面,现有一白球A和一彩球B,在图中的GH边上找一点O,当击打白球A时,使白球A碰撞台边GH上的O点,反弹后能击中彩球B.
如图,四边形EFGH为长方形的台球桌面,现有一白球A和一彩球B,在图中的GH边上找一点O,当击打白球A时,使白球A碰撞台边GH上的O点,反弹后能击中彩球B. 如图,三角板ABC中,∠ACB=90°,AB=2,∠A=30°,三角板ABC绕直角顶点C顺时针旋转90°得到△A1B1C,求:
如图,三角板ABC中,∠ACB=90°,AB=2,∠A=30°,三角板ABC绕直角顶点C顺时针旋转90°得到△A1B1C,求:
 在正方形ABCD各边上一次截取AE=BF=CG=DH,连接EF,FG,GH,HE.试问四边形EFGH是否是正方形?
在正方形ABCD各边上一次截取AE=BF=CG=DH,连接EF,FG,GH,HE.试问四边形EFGH是否是正方形? 如图,已知点A是双曲线y=
如图,已知点A是双曲线y=