题目内容
13.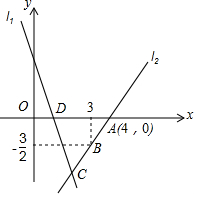 如图,直线l1的表达式为y=-3x+3,且与x轴交于点D,直线l2经过点A(4,0),B(3,-$\frac{3}{2}$),直线l1,l2交于点C.
如图,直线l1的表达式为y=-3x+3,且与x轴交于点D,直线l2经过点A(4,0),B(3,-$\frac{3}{2}$),直线l1,l2交于点C.(1)求直线l2的表达式;
(2)在直线l2上存在点P,能使S△ADP=2S△ACD,求点P的坐标.
分析 (1)设直线l2的表达式为:y=kx+b,解方程组即可得到结论;
(2)根据直线l1的解析式y=-3x+3求得D(1,0),解方程组得到C(2,-3),设P(m,$\frac{3}{2}$m-6),根据S△ADP=2S△ACD列方程即可得到结论.
解答 解:(1)设直线l2的表达式为:y=kx+b,
∵直线l2经过点A(4,0),B(3,-$\frac{3}{2}$),
∴$\left\{\begin{array}{l}{0=4k+b}\\{-\frac{3}{2}=3k+b}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=\frac{3}{2}}\\{b=-6}\end{array}\right.$,
∴直线l2的表达式为:y=$\frac{3}{2}$x-6;
(2)∵直线l1y=-3x+3与x轴交于点D,
∴D(1,0),
解$\left\{\begin{array}{l}{y=\frac{3}{2}x-6}\\{y=-3x+3}\end{array}\right.$得$\left\{\begin{array}{l}{x=2}\\{y=-3}\end{array}\right.$,
∴C(2,-3),
设P(m,$\frac{3}{2}$m-6),
∵S△ADP=2S△ACD,
∴$\frac{1}{2}$×2×($\frac{3}{2}$m-6)=2×$\frac{1}{2}$×2×3,
∴m=8,
∴点P的坐标(8,6).
点评 本题考查了两条直线平行或相交问题,待定系数法求函数的解析式,三角形面积的计算,正确的识别图形是解题的关键.

练习册系列答案
相关题目
8. 符合数轴所表示的解集的不等式组是( )
符合数轴所表示的解集的不等式组是( )
 符合数轴所表示的解集的不等式组是( )
符合数轴所表示的解集的不等式组是( )| A. | $\left\{\begin{array}{l}{x+1>0}\\{4-x>0}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+1>0}\\{x-4>0}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+1<0}\\{x-4>0}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+1<0}\\{4-x>0}\end{array}\right.$ |
2.永州市是一个降水丰富的地区,今年4月初,某地连续降雨导致该地某水库水位持续上涨,下表是该水库4月1日~4月4日的水位变化情况:
(1)请建立该水库水位y与日期x之间的函数模型;
(2)请用求出的函数表达式预测该水库今年4月6日的水位;
(3)你能用求出的函数表达式预测该水库今年12月1日的水位吗?
| 日期x | 1 | 2 | 3 | 4 |
| 水位y(米) | 20.00 | 20.50 | 21.00 | 21.50 |
(2)请用求出的函数表达式预测该水库今年4月6日的水位;
(3)你能用求出的函数表达式预测该水库今年12月1日的水位吗?
13.某登山队从大本营出发,在向上攀登的过程中,测得所在位置的气温y℃与向上攀登的高度x km的几组对应值如表:
若每向上攀登1km,所在位置的气温下降幅度基本一致,则向上攀登的海拔高度为2.5km时,登山队所在位置的气温约为-10℃.
| 向上攀登的高度x/km | 0.5 | 1.0 | 1.5 | 2.0 |
| 气温y/℃ | 2.0 | -0.9 | -4.1 | -7.0 |
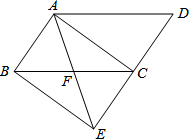 如图,将?ABCD的边DC延长至点E,使DC=CE,连接AE,交边BC于点F.
如图,将?ABCD的边DC延长至点E,使DC=CE,连接AE,交边BC于点F.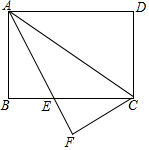 如图,在矩形ABCD中,AB=4,BC=8,将矩形沿AC折叠,点D落在点F处,AF与BC交于点E.
如图,在矩形ABCD中,AB=4,BC=8,将矩形沿AC折叠,点D落在点F处,AF与BC交于点E.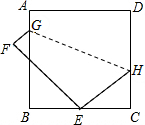 如图,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH.若BE:EC=2:1,求线段EC,CH的长.
如图,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH.若BE:EC=2:1,求线段EC,CH的长.