题目内容
10.一个凸多边形共有20条对角线,它是几边形?是否存在有15条对角线的多边形?如果存在,它是几边形?如果不存在,说明得出结论的过程.分析 利用多边形对角线公式:对角线的条数=$\frac{n(n-3)}{2}$列出方程,然后求得方程的解,从而可做出判断.
解答 解:设这个多边形是n边形,则
∵$\frac{n(n-3)}{2}$=20,
∴n2-3n-40=0,
(n-8)(n+5)=0,
解得n=8,n=-5(舍去),
故多边形的边数为8;
∵$\frac{n(n-3)}{2}$=15,
∴n2-3n-30=0,
∵b2-4ac=9+120=129,
∴方程的根,无法求出整数,
故这样的多边形不存在.
点评 此题主要考查了多边形对角线公式,熟练记忆公式是解题关键.

练习册系列答案
相关题目
2.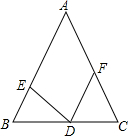 如图所示,在△ABC中,D,E,F分别在BC,AB,AC上,且AB=AC,BE=CD,BD=CF,则∠EDF等于( )
如图所示,在△ABC中,D,E,F分别在BC,AB,AC上,且AB=AC,BE=CD,BD=CF,则∠EDF等于( )
 如图所示,在△ABC中,D,E,F分别在BC,AB,AC上,且AB=AC,BE=CD,BD=CF,则∠EDF等于( )
如图所示,在△ABC中,D,E,F分别在BC,AB,AC上,且AB=AC,BE=CD,BD=CF,则∠EDF等于( )| A. | 180°-2∠B | B. | 180°-∠B | C. | ∠B | D. | 90°-∠B |
 如图:在△ABC中,∠BAC=60°,∠1=∠2,∠3=∠4,求∠DAC的度数?
如图:在△ABC中,∠BAC=60°,∠1=∠2,∠3=∠4,求∠DAC的度数?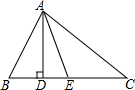 如图,在△ABC中,∠B=60°,∠C=40°,AD⊥BC于D,AE平分∠BAC;则∠DAE=10°.
如图,在△ABC中,∠B=60°,∠C=40°,AD⊥BC于D,AE平分∠BAC;则∠DAE=10°.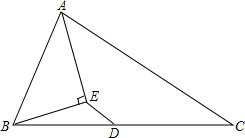 如图,△ABC中,D是BC边的中点,AE平分∠BAC,BE⊥AE于E,若AB=5,AC=7,求ED.
如图,△ABC中,D是BC边的中点,AE平分∠BAC,BE⊥AE于E,若AB=5,AC=7,求ED.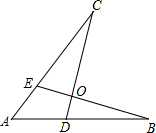 如图.下面四个条件中,请你选出三个,以其中两个为已知条件,另一个为求证,编一道题并证明(只需写出一种情况).①AE=AD;②AB=AC;③OB=OC;④∠B=∠C.
如图.下面四个条件中,请你选出三个,以其中两个为已知条件,另一个为求证,编一道题并证明(只需写出一种情况).①AE=AD;②AB=AC;③OB=OC;④∠B=∠C.