题目内容
(1)解方程:x2+8x-4=0
(2)解不等式组
.
(2)解不等式组
|
考点:解一元二次方程-配方法,解一元一次不等式组
专题:
分析:(1)首先移项,然后在方程的左右两边同时加上一次项系数一半的平方,左边就是完全平方式,右边就是常数,然后利用平方根的定义即可求解.
(2)先计算不等式组中的每一个不等式,然后求其交集即可.
(2)先计算不等式组中的每一个不等式,然后求其交集即可.
解答:解:(1)移项,得x2+8x=4.
两边同加上42,得x2+8x+16=4+16,
即(x+4)2=20.
利用开平方法,得
x+4=2
或x+4=2
.
解得x=-4+2
或x=-4-2
.
所以,原方程的根是x1=-4+2
,x2=-4-2
.
(2)
.
解不等式(a)得 x>1.
解不等式(b)得 x≤4,
则原不等式组的解集是:1<x≤4.
两边同加上42,得x2+8x+16=4+16,
即(x+4)2=20.
利用开平方法,得
x+4=2
| 5 |
| 5 |
解得x=-4+2
| 5 |
| 5 |
所以,原方程的根是x1=-4+2
| 5 |
| 5 |
(2)
|
解不等式(a)得 x>1.
解不等式(b)得 x≤4,
则原不等式组的解集是:1<x≤4.
点评:本题考查了解一元二次方程-配方法.配方法的一般步骤:
(1)把常数项移到等号的右边;
(2)把二次项的系数化为1;
(3)等式两边同时加上一次项系数一半的平方.
选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.
(1)把常数项移到等号的右边;
(2)把二次项的系数化为1;
(3)等式两边同时加上一次项系数一半的平方.
选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.

练习册系列答案
相关题目
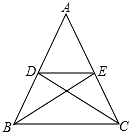 在等腰三角形ABC中,AB=AC,BE,CD分别是底角的平分线,DE∥BC,图中等腰三角形的个数有( )
在等腰三角形ABC中,AB=AC,BE,CD分别是底角的平分线,DE∥BC,图中等腰三角形的个数有( )| A、4个 | B、5个 | C、6个 | D、8个 |