题目内容
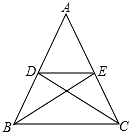在等腰三角形ABC中，AB=AC，BE，CD分别是底角的平分线，DE∥BC，图中等腰三角形的个数有（ ）| A、4个 | B、5个 | C、6个 | D、8个 |
考点：等腰三角形的判定与性质
专题：
分析：如图，证明∠DBE=∠DEB，∠EDC=∠ECD，∠ODE=∠OED，∠OBC=∠OCB，进而得到AD=AE、OD=OE、OB=OC、BD=ED、CE=DE，即可解决问题．
解答：
解：如图，∵AB=AC，
∴∠ABC=∠ACB（设为2α）；
∵DE∥BC，
∴∠ADE=∠AED=2α；∠DEO=∠CBO=α，∠EDO=∠BCO=α；
∵BE，CD分别是底角的平分线，
∴∠ABE=∠CBE=α，∠ACD=∠BCD=α，
∴∠DBE=∠DEB，∠EDC=∠ECD，∠ODE=∠OED，∠OBC=∠OCB，
∴AD=AE、OD=OE、OB=OC、BD=ED、CE=DE，
∴图中共有6个等腰三角形，
故选C．
解：如图，∵AB=AC，∴∠ABC=∠ACB（设为2α）；
∵DE∥BC，
∴∠ADE=∠AED=2α；∠DEO=∠CBO=α，∠EDO=∠BCO=α；
∵BE，CD分别是底角的平分线，
∴∠ABE=∠CBE=α，∠ACD=∠BCD=α，
∴∠DBE=∠DEB，∠EDC=∠ECD，∠ODE=∠OED，∠OBC=∠OCB，
∴AD=AE、OD=OE、OB=OC、BD=ED、CE=DE，
∴图中共有6个等腰三角形，
故选C．
点评：该题主要考查了等腰三角形的判定及其性质的应用问题；同时还渗透了对平行线的性质等几何知识点的考查；应牢固掌握等腰三角形的判定及其性质．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
如图，AB∥CD，CE平分∠ACD交AB于E点．
已知如图，∠1=∠2，∠3=∠4，四边形ABCD是不是平行四边形？为什么？
把四个棱长为1cm的正方体按图堆放墙角，将其外面涂一层漆，则其涂漆面积为