题目内容
已知:x+y=3,xy=1,求:
(1)4x+4y
(2)(x-y)2
(3)x3+y3.
(1)4x+4y
(2)(x-y)2
(3)x3+y3.
考点:完全平方公式
专题:计算题
分析:(1)原式利用提取4变形后,把x+y的值代入计算即可求出值;
(2)原式利用完全平方公式变形,把x+y与xy的值代入计算即可求出值;
(3)原式利用立方和公式变形,将各自的值代入计算即可求出值.
(2)原式利用完全平方公式变形,把x+y与xy的值代入计算即可求出值;
(3)原式利用立方和公式变形,将各自的值代入计算即可求出值.
解答:解:(1)∵x+y=3,
∴原式=4(x+y)=12;
(2)∵x+y=3,xy=1,
∴(x-y)2=(x+y)2-4xy=9-4=5;
(3)把x+y=3两边平方得:(x+y)2=x2+y2+2xy=9,
将xy=1代入得:x2+y2=7,
则x3+y3=(x+y)(x2+y2-xy)=18.
∴原式=4(x+y)=12;
(2)∵x+y=3,xy=1,
∴(x-y)2=(x+y)2-4xy=9-4=5;
(3)把x+y=3两边平方得:(x+y)2=x2+y2+2xy=9,
将xy=1代入得:x2+y2=7,
则x3+y3=(x+y)(x2+y2-xy)=18.
点评:此题考查了完全平方公式,熟练掌握公式是解本题的关键.

练习册系列答案
相关题目
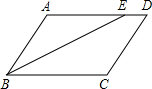 在?ABCD中,AB=6cm,AD=8cm,BE平分∠ABC,求DE的长度.
在?ABCD中,AB=6cm,AD=8cm,BE平分∠ABC,求DE的长度. 已知AB∥DE,∠B=∠E,说明BC∥EF.
已知AB∥DE,∠B=∠E,说明BC∥EF. 已知:如图,?ABCD中,M为BC中点,∠MBC=∠MCB.求证:四边形ABCD是矩形.
已知:如图,?ABCD中,M为BC中点,∠MBC=∠MCB.求证:四边形ABCD是矩形. 用代表式表示如图所示正方形中阴影部分面积S,并求出a=5cm时,阴影部分的面积S(π取3)
用代表式表示如图所示正方形中阴影部分面积S,并求出a=5cm时,阴影部分的面积S(π取3)