题目内容
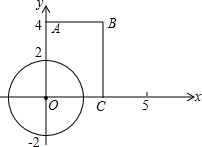 如图直角坐标系中,矩形ABCO,边AO、CO在坐标轴上,点B的坐标是(3,4),☉O半径为2.
如图直角坐标系中,矩形ABCO,边AO、CO在坐标轴上,点B的坐标是(3,4),☉O半径为2.(1)连接AC,判断AC的中点与☉O的位置关系;
(2)若将矩形ABCO沿着过A点的直线翻折,使得AB边所在直线翻折后能与☉O相切,求折痕的函数关系式.
考点:圆的综合题
专题:
分析:(1)连接AC、BD交于点D,由矩形的性质可求得OD=
AC=2.5,从而可判断出点D于⊙O的关系;
(2)设翻折后的直线与圆相切于点E,分翻折后的直线AE在第二象限和在第一象限与圆相切两种情况,再根据折痕为直线AB和AE两直线的夹角的平分线求出折痕与x轴的交点坐标,根据y=kx+b,求出其解析式即可.
| 1 |
| 2 |
(2)设翻折后的直线与圆相切于点E,分翻折后的直线AE在第二象限和在第一象限与圆相切两种情况,再根据折痕为直线AB和AE两直线的夹角的平分线求出折痕与x轴的交点坐标,根据y=kx+b,求出其解析式即可.
解答:解:(1)如图1,连接AC、BD交于点D,由矩形的性质可知D点为AC的中点,
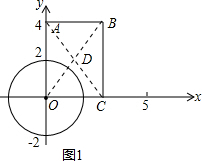
在Rt△AOC中可求得AC=5,
所以OD=
AC=2.5>2,所以点D在⊙O外,
即AC的中点在⊙O外;
(2)设翻折后AB与⊙O相切于点E,
当E点在第二象限时,如图2,连接OE,设折痕所在的直线交x轴于点F,
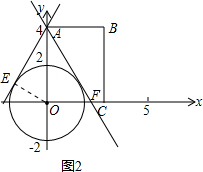
由题意可知∠BAF=∠AEF,
而在Rt△OEA中,OE=2,OA=4,
∴∠EAO=30°,而∠OAB=90°,
∴∠FAB=60°,
∴∠OAF=30°,
在Rt△OAF中,OA=4,设OF=x,则AF=2x,由勾股定理可得:x2+42=(2x)2,
解得x=
,此时F点坐标为(
,0),
设直线AF的解析式为y=kx+4,把点F坐标代入可解得k=-
,
∴折痕的函数关系式为:y=-
x+4,
当E点在第一象限时,如图3,连接OE,设折痕与x轴交于点F,
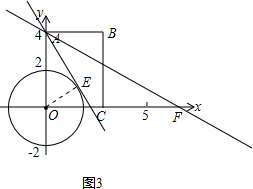
在Rt△OAE中,OE=2,OA=4,
∴∠OAE=30°,
∴∠EAB=60°,
∴∠EAF=30°,
∴∠OAF=60°,
在Rt△OAF中,OA=4,则OF=4
,即F点坐标为(4
,0),
设折痕的函数关系式为y=kx+4,把F点坐标代入可解得k=-
,
∴折痕的函数关系式为:y=-
x+4,
综上可知折痕的函数关系式为y=-
x+4或y=-
x+4.

在Rt△AOC中可求得AC=5,
所以OD=
| 1 |
| 2 |
即AC的中点在⊙O外;
(2)设翻折后AB与⊙O相切于点E,
当E点在第二象限时,如图2,连接OE,设折痕所在的直线交x轴于点F,

由题意可知∠BAF=∠AEF,
而在Rt△OEA中,OE=2,OA=4,
∴∠EAO=30°,而∠OAB=90°,
∴∠FAB=60°,
∴∠OAF=30°,
在Rt△OAF中,OA=4,设OF=x,则AF=2x,由勾股定理可得:x2+42=(2x)2,
解得x=
4
| ||
| 3 |
4
| ||
| 3 |
设直线AF的解析式为y=kx+4,把点F坐标代入可解得k=-
| 3 |
∴折痕的函数关系式为:y=-
| 3 |
当E点在第一象限时,如图3,连接OE,设折痕与x轴交于点F,

在Rt△OAE中,OE=2,OA=4,
∴∠OAE=30°,
∴∠EAB=60°,
∴∠EAF=30°,
∴∠OAF=60°,
在Rt△OAF中,OA=4,则OF=4
| 3 |
| 3 |
设折痕的函数关系式为y=kx+4,把F点坐标代入可解得k=-
| ||
| 3 |
∴折痕的函数关系式为:y=-
| ||
| 3 |
综上可知折痕的函数关系式为y=-
| 3 |
| ||
| 3 |
点评:本题主要考查点和圆的位置关系、切线的性质及解直角三角形、待定系数法求函数解析式等的综合应用,在第(2)问中利用翻折得到折痕即为AB和切线夹角的平分线从而确定出折痕的位置是解题的关键.

练习册系列答案
相关题目
若m是方程x2-2014x-1=0的根,则(m2-2014m+3)(m2-2014m+4)的值为( )
| A、16 | B、12 | C、20 | D、30 |
 +(4y2-3xy),其中x=-1,y=-
+(4y2-3xy),其中x=-1,y=-
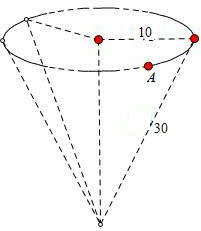 圆锥底面半径OA=10,母线=30,一只蚂蚁从A点出发,绕侧面一周回到A点,最短路径是多少?
圆锥底面半径OA=10,母线=30,一只蚂蚁从A点出发,绕侧面一周回到A点,最短路径是多少?