题目内容
14.已知二次函数y=mx2-5mx+1(m为常数,m>0),设该函数的图象与y轴交于点A,该图象上的一点B与点A关于该函数图象的对称轴对称.(1)求点A,B的坐标;
(2)点O为坐标原点,点M为该函数图象的对称轴上一动点,求当M运动到何处时,△MAO的周长最小.
分析 (1)令x=0可求得y=1,可求得A点坐标,再利用对称性可求得B点坐标;
(2)可先求得直线OB解析式,当点M运动到直线OB与二次函数对称轴的交点时,满足条件,可求得M点的坐标.
解答 解:∵
(1)当x=0时,y=1,则点A的坐标为(0,1),
∵抛物线对称轴为x=$\frac{5m}{2m}$=$\frac{5}{2}$,
∴B点坐标为(5,1);
(2)设直线OB解析式为y=kx,把B(5,1)代入可得5k=1,解得k=$\frac{1}{5}$,
∴直线OB解析式为y=$\frac{1}{5}$x,
由轴对称的性质可知当点M运动到直线OB与二次函数对称轴的交点时,△MAO的周长最小.
当x=$\frac{5}{2}$时,y=$\frac{1}{2}$,
∴M点的坐标为($\frac{5}{2}$,$\frac{1}{2}$).
点评 本题主要考查二次函数的性质及轴对称的性质,利用轴对称的性质确定出M点的位置是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2. 如图,已知在△ABC中,cosA=$\frac{1}{3}$,BE、CF分别是AC、AB边上的高,联结EF,那么△AEF和△ABC的周长比为( )
如图,已知在△ABC中,cosA=$\frac{1}{3}$,BE、CF分别是AC、AB边上的高,联结EF,那么△AEF和△ABC的周长比为( )
 如图,已知在△ABC中,cosA=$\frac{1}{3}$,BE、CF分别是AC、AB边上的高,联结EF,那么△AEF和△ABC的周长比为( )
如图,已知在△ABC中,cosA=$\frac{1}{3}$,BE、CF分别是AC、AB边上的高,联结EF,那么△AEF和△ABC的周长比为( )| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 1:9 |
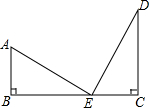 如图所示,有两根直杆隔河相对,一杆高30m,另一杆高20m,两杆相距50m.现两杆上各有一只鱼鹰,他们同时看到两杆之间的河面上E处浮起一条小鱼于是以同样的速度同时飞下来夺鱼结果两只鱼鹰同时到达,叼住小鱼.问,两杆底部距鱼的距离各是多少?
如图所示,有两根直杆隔河相对,一杆高30m,另一杆高20m,两杆相距50m.现两杆上各有一只鱼鹰,他们同时看到两杆之间的河面上E处浮起一条小鱼于是以同样的速度同时飞下来夺鱼结果两只鱼鹰同时到达,叼住小鱼.问,两杆底部距鱼的距离各是多少?