题目内容
 已知一个直角三角形纸片OAB,其中∠AOB=90°,OA=2,OB=4,如图所示,将该纸片放置在平面直角坐标系中,折叠该纸片,折痕与边OB交于点C,与边AB交于点D.
已知一个直角三角形纸片OAB,其中∠AOB=90°,OA=2,OB=4,如图所示,将该纸片放置在平面直角坐标系中,折叠该纸片,折痕与边OB交于点C,与边AB交于点D.(1)若折叠后使点B与点A重合,求点D的坐标;
(2)若折叠后点B落在边OA上的点为B′,且使B′D∥OB,此时你能否判断出B′C和AB的位置关系?若能,给出证明;若不能,试说出理由.
考点:翻折变换(折叠问题),坐标与图形性质
专题:
分析:(1)根据折叠变换的性质,点D为线段AB的中点,而A、B两点的坐标为A(2,0)、B(0,4),运用中点的坐标公式即可解决问题.
(2)由题意知BP=B′P;由B′D∥OB,得到△BCP∽△B′DP,
=
=1,故BC=B′D,四边形BCB′D为平行四边形,问题即可解决.
(2)由题意知BP=B′P;由B′D∥OB,得到△BCP∽△B′DP,
| BC |
| B′D |
| BP |
| B′P |
解答: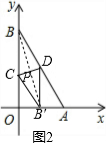
 解:(1)如图1,由题意得:
解:(1)如图1,由题意得:
点D为线段AB的中点,A、B两点的坐标分别为A(2,0),B(0,4),
设D点的坐标为(λ,μ),则λ=
=1,μ=
=2,
∴D点的坐标为(1,2).
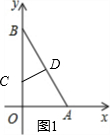
(2)B′C∥AB.理由如下:
如图2,连接BB′,交CD于点P;
则BP=B′P;
∵B′D∥OB,
∴△BCP∽△B′DP,
∴
=
=1,
∴BC=B′D,而B′D∥OB,
∴四边形BCB′D为平行四边形,
∴B′C∥AB.

 解:(1)如图1,由题意得:
解:(1)如图1,由题意得:点D为线段AB的中点,A、B两点的坐标分别为A(2,0),B(0,4),
设D点的坐标为(λ,μ),则λ=
| 2+0 |
| 2 |
| 4+0 |
| 2 |
∴D点的坐标为(1,2).
(2)B′C∥AB.理由如下:
如图2,连接BB′,交CD于点P;
则BP=B′P;
∵B′D∥OB,
∴△BCP∽△B′DP,
∴
| BC |
| B′D |
| BP |
| B′P |
∴BC=B′D,而B′D∥OB,
∴四边形BCB′D为平行四边形,
∴B′C∥AB.
点评:该题以平面直角坐标系为载体,以翻折变换为方法,以考查坐标与图形的性质、平行线的判定等几何知识点为核心构造而成;对分析问题解决问题的能力提出了较高的要求.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
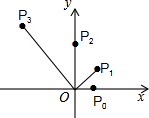 如图,在平面直角坐标系中,已知点P0的坐标为(1,0)将线段OP按逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1,又将线段OP1按逆时针方向旋转45°,再将其长度伸长为OP1的2倍得到线段OP2;…;如此进行下去,得到线段OP3,OP4,…OPn(n为正整数)则点P2015的坐标为( )
如图,在平面直角坐标系中,已知点P0的坐标为(1,0)将线段OP按逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1,又将线段OP1按逆时针方向旋转45°,再将其长度伸长为OP1的2倍得到线段OP2;…;如此进行下去,得到线段OP3,OP4,…OPn(n为正整数)则点P2015的坐标为( )A、(22014•
| ||||
B、(22012•
| ||||
C、(-22013•
| ||||
| D、(0,-22014) |
已知A(-1,y1),B(1,y2),C(2,y3)三点在抛物线y=x2-2x+m上,则y1、y2、y3的大小关系为( )
| A、y1<y2<y3 |
| B、y3<y2<y1 |
| C、y2<y1<y3 |
| D、y2<y3<y1 |
 如图,已知AB=AC,且DC⊥AC,DB⊥AB,求证:AD平分∠CAB.
如图,已知AB=AC,且DC⊥AC,DB⊥AB,求证:AD平分∠CAB.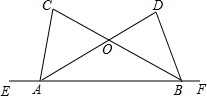 如图,点E、A、B、F在同一条直线上,AD与BC交于点O,已知∠CAE=∠DBF,AC=BD.求证:
如图,点E、A、B、F在同一条直线上,AD与BC交于点O,已知∠CAE=∠DBF,AC=BD.求证: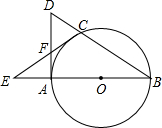 如图,AB是⊙O的直径,C是⊙O上的一点,过点A作DA⊥BA于点A,交BC的延长线于点D,延长BA至点E,连接CE交DA于点F,恰使AF=DF
如图,AB是⊙O的直径,C是⊙O上的一点,过点A作DA⊥BA于点A,交BC的延长线于点D,延长BA至点E,连接CE交DA于点F,恰使AF=DF 如图,AB=AC,AD=AE,∠BAC=∠DAE,∠1=21°,∠2=29°,则∠3=
如图,AB=AC,AD=AE,∠BAC=∠DAE,∠1=21°,∠2=29°,则∠3=