题目内容
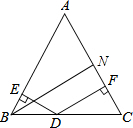 △ABC是等边三角形,点D是BC边上的任意一点,DE⊥AB于点E,DF⊥AC于点F,BN⊥AC于点N,则DE,DF,BN三者的数量关系为
△ABC是等边三角形,点D是BC边上的任意一点,DE⊥AB于点E,DF⊥AC于点F,BN⊥AC于点N,则DE,DF,BN三者的数量关系为考点:等边三角形的性质,三角形的面积
专题:
分析:连接AD,利用三角形的面积相等结合等边三角形的性质可得到BN=DE+DF.
解答: 解:BN=DE+DF,证明如下:
解:BN=DE+DF,证明如下:
连接AD,
∵S△ABC=S△ABD+S△ACD,
∴
AC•BN=
AB•DE+
AC•DF,
∵△ABC为等边三角形,
∴AB=AC,
∴AC•BN=AC•DE+AC•DF,
∴BN=DE+DF.
故答案为:BN=DE+DF.
 解:BN=DE+DF,证明如下:
解:BN=DE+DF,证明如下:连接AD,
∵S△ABC=S△ABD+S△ACD,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵△ABC为等边三角形,
∴AB=AC,
∴AC•BN=AC•DE+AC•DF,
∴BN=DE+DF.
故答案为:BN=DE+DF.
点评:本题主要考查等边三角形的性质,利用等积法得到
AC•BN=
AB•DE+
AC•DF是解题的关键.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |

练习册系列答案
相关题目
已知A(-1,y1),B(1,y2),C(2,y3)三点在抛物线y=x2-2x+m上,则y1、y2、y3的大小关系为( )
| A、y1<y2<y3 |
| B、y3<y2<y1 |
| C、y2<y1<y3 |
| D、y2<y3<y1 |
若x≠0,则
+
=( )
| |x| |
| x |
| x |
| |x| |
| A、-1或1 | B、0 |
| C、1 | D、-2或2 |
 如图,在⊙O中,AD是直径,∠ABC=40°,则∠CAD等于( )
如图,在⊙O中,AD是直径,∠ABC=40°,则∠CAD等于( )| A、40° | B、50° |
| C、60° | D、70° |
下列运算正确的是( )
| A、a5•a3=a15 |
| B、6a2m÷2am=3a2 |
| C、(-a5)2=a10 |
| D、a6÷a3=a2 |
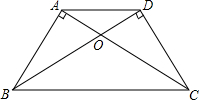 如图,AB⊥AC,DC⊥DB,填空:
如图,AB⊥AC,DC⊥DB,填空: 如图,AB=AC,AD=AE,∠BAC=∠DAE,∠1=21°,∠2=29°,则∠3=
如图,AB=AC,AD=AE,∠BAC=∠DAE,∠1=21°,∠2=29°,则∠3= 如图,AB是半圆O的直径,过⊙O上一点C,作CD⊥AB于点D.已知AC=3cm,BC=5cm,则AB=
如图,AB是半圆O的直径,过⊙O上一点C,作CD⊥AB于点D.已知AC=3cm,BC=5cm,则AB=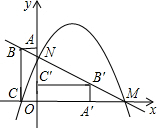 如图,在平面直角坐系中,矩形OABC的顶点A(0,3),C(-1,0).将矩形OABC绕原点顺时针旋转90°,得到矩形OA′B′C′.设直线BB′与x轴交于点M、与y轴交于点N,抛物线y=ax2+2x+c的图象经过点C、M、N.解答下列问题:
如图,在平面直角坐系中,矩形OABC的顶点A(0,3),C(-1,0).将矩形OABC绕原点顺时针旋转90°,得到矩形OA′B′C′.设直线BB′与x轴交于点M、与y轴交于点N,抛物线y=ax2+2x+c的图象经过点C、M、N.解答下列问题: