题目内容
 如图,△ABC是圆O的内接三角形,若∠OBC=70°,则∠A的度数是( )
如图,△ABC是圆O的内接三角形,若∠OBC=70°,则∠A的度数是( )| A、20° | B、25° |
| C、30° | D、35° |
考点:圆周角定理,等腰三角形的性质
专题:
分析:先由OB=OC,得∠OCB=∠OBC=70°,因此∠COB=180°-70°-70°=40°,再由圆周角定理得到∠A=
∠COB.
| 1 |
| 2 |
解答: 解:∵OB=OC,∠OBC=70°,
解:∵OB=OC,∠OBC=70°,
∴∠OCB=∠OBC=70°,
∴∠COB=180°-70°-70°=40°,
∴∠A=
∠COB=
×40°=20°.
故选A.
 解:∵OB=OC,∠OBC=70°,
解:∵OB=OC,∠OBC=70°,∴∠OCB=∠OBC=70°,
∴∠COB=180°-70°-70°=40°,
∴∠A=
| 1 |
| 2 |
| 1 |
| 2 |
故选A.
点评:本题考查了圆周角定理.在同圆或等圆中,同弧或等弧所对的圆周角相等,一条弧所对的圆周角是它所对的圆心角的一半.也考查了等腰三角形的性质和三角形的内角和定理.

练习册系列答案
相关题目
下列说法错误的是( )
| A、三角形的中线、高、角平分线都是线段 |
| B、任意三角形内角和都是180° |
| C、三角形按角可分为锐角三角形、直角三角形和等腰三角形 |
| D、三角形内,到三角形三边距离相等的点是三角形三条角平分线的交点 |
下列判断中正确的是( )
| A、6a2bc与bca2不是同类项 | ||
B、
| ||
| C、25xyz是三次单项式 | ||
| D、3x2-y+5xy2是二次三项式 |
 如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=35°,则∠2的度数为
如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=35°,则∠2的度数为 如图,直线AB与CD相交于点O,OE平分∠BOD.
如图,直线AB与CD相交于点O,OE平分∠BOD.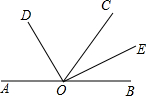 如图,A、O、B三点在同一直线上,OC是任一条射线,OD、OE分别是∠AOC和∠BOC的平分线.
如图,A、O、B三点在同一直线上,OC是任一条射线,OD、OE分别是∠AOC和∠BOC的平分线. 如图,已知:EF∥CD,∠1+∠2=180°,试判断∠BGD与∠BCA的大小,并给予证明.
如图,已知:EF∥CD,∠1+∠2=180°,试判断∠BGD与∠BCA的大小,并给予证明. 如图,在⊙O中直径CD垂直弦AB,垂足为E,若∠AOD=52°,则∠DCB=
如图,在⊙O中直径CD垂直弦AB,垂足为E,若∠AOD=52°,则∠DCB=