题目内容
13．开口向下的抛物线y=（m2-2）x2+2mx+1的对称轴是直线x=-1，则m=-1．分析 直接利用二次函数对称轴公式求出m的值，再利用其开口方向得出符合题意的m的值．
解答 解：∵开口向下的抛物线y=（m2-2）x2+2mx+1的对称轴是直线x=-1，
∴m2-2＜0，x=-$\frac{b}{2a}$=-$\frac{2m}{2（{m}^{2}-2）}$=-1，
解得：m1=-1，m2=2，
当m=2时，m2-2＞0，
故m=-1．
故答案为：-1．
点评 此题主要考查了二次函数的性质，根据题意得出二次函数对称轴公式m的值是解题关键．
练习册系列答案
相关题目
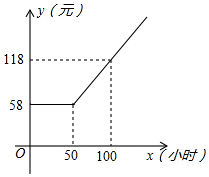某广电局与长江证券公司联合推出光电宽带网业务，用户通过宽带网可以享受新闻点播、影视欣赏、股市大户室等项服务，用户缴纳每月上网费y（元）与上网时间x（小时）的函数关系用如图所示的折线表示．