题目内容
3.某工厂现有甲种原料360千克,乙种原料290千克,计划用这两种原料生产A、B两种产品共50件.已知生产1件A种产品需甲种原料9千克,乙种原料3千克,可获利700元;生产1件B种产品需甲种原料4千克,乙种原料10千克,可获利1200元.设生产A、B两种产品可获总利润是y元,其中A种产品的生产件数是x.(1)写出y与x之间的函数关系式;
(2)符合题意的生产方案有几种?请你帮忙设计出来;
(3)如何安排A、B两种产品的生产件数,使总利润y有最大值,并求出y的最大值.
分析 (1)根据总利润=A种产品的利润+B种产品的利润即可计算.
(2)列出不等式组即可解决问题.
(3)利用一次函数的增减性,即可解决问题.
解答 解:(1)∵A种产品的生产件数是x,B种产品的生产件数是(50-x),
由题意:y=700x+1200(50-x)=-500x+60000.
(2)由题意:$\left\{\begin{array}{l}{9x+4(50-x)≤360}\\{3x+10(50-x)≤290}\end{array}\right.$解得30≤x≤32,
∵x为众数,
∴x=30,31,32.
∴生产方案有3种:
方案1:A种产品:30件,B种产品20件.
方案2:A种产品:31件,B种产品19件.
方案3:A种产品:32件,B种产品18件.
(3)在y=-500x+60000中,
∵-500<0,
∴y随x增加而减小,
∴x=30时,y有最大值=-500×30+60000=45000元.
点评 本题考查一次函数的应用,一元一次不等式组等知识,解题的关键是理解题意,学会利用不等式解决实际问题,学会利用一次函数的增减性解决最值问题,属于中考常考题型.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
15.比$\sqrt{5}$大的数是( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | $\frac{5}{2}$ |
11.为鼓励居民节约用水,某市决定对居民用水收费实行“阶梯价”,即当每月用水量不超过15吨时,采用基本价收费;当每月用水量超过15吨时,超过部分每吨采用市场价收费.小兰家四、五月份的用水量及收费情况如下表:
(1)求该市每吨水的基本价和市场价.
(2)设每月用水量为n吨,应缴水费为m元,请写出m与n之间的函数关系式.
(3)小兰家6月份的用水量为26吨,则她家要缴水费多少元?
(4)若小兰家7月份的水费为165元,则她家7月份用水多少吨?
| 月份 | 用水量(吨) | 水费(元) |
| 4 | 22 | 51 |
| 5 | 20 | 45 |
(2)设每月用水量为n吨,应缴水费为m元,请写出m与n之间的函数关系式.
(3)小兰家6月份的用水量为26吨,则她家要缴水费多少元?
(4)若小兰家7月份的水费为165元,则她家7月份用水多少吨?
 某几何体的三视图如图所示,则组成该几何体的小正方体的个数是5.
某几何体的三视图如图所示,则组成该几何体的小正方体的个数是5.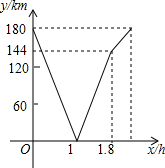 一辆货车从A地去B地,一辆轿车从B地去A地,同时出发,匀速行驶,各自到达终点后停止,轿车的速度大于货车的速度.两辆车之间的距离为y(km)与货车行驶的时间为x(h)之间的函数关系如图所示.
一辆货车从A地去B地,一辆轿车从B地去A地,同时出发,匀速行驶,各自到达终点后停止,轿车的速度大于货车的速度.两辆车之间的距离为y(km)与货车行驶的时间为x(h)之间的函数关系如图所示.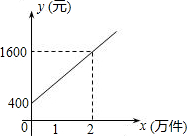 某公司市场营销部的营销员的个人月收入与该营销员每月的销量成一次函数关系,其图象如图所示.根据图象提供的信息,解答下列问题:
某公司市场营销部的营销员的个人月收入与该营销员每月的销量成一次函数关系,其图象如图所示.根据图象提供的信息,解答下列问题: