题目内容
4.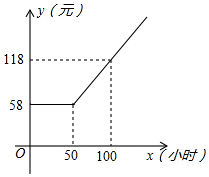 某广电局与长江证券公司联合推出光电宽带网业务,用户通过宽带网可以享受新闻点播、影视欣赏、股市大户室等项服务,用户缴纳每月上网费y(元)与上网时间x(小时)的函数关系用如图所示的折线表示.
某广电局与长江证券公司联合推出光电宽带网业务,用户通过宽带网可以享受新闻点播、影视欣赏、股市大户室等项服务,用户缴纳每月上网费y(元)与上网时间x(小时)的函数关系用如图所示的折线表示.(1)若小明家四月上网45小时,应交上网费58元.
(2)求用户缴纳每月上网费y(元)与上网时间x(小时)的函数关系式;
(3)若小聪家某月交上网费70元,问该月上网时间是多少小时?
分析 (1)由于上网时间小于50小时,由图象知,应交58元;
(2)根据月上网费=每小时的收费×上网时间可得出函数关系式;
(3)由于70>58,把y=70代入y=1.2x-2计算结论.
解答 (1)∵x=45<50,由图象知,y=58,
故答案为:58;
(2)当x≤50时,y=58
当x>50时,设y与x的关系式是y=kx+b
由题意得:$\left\{\begin{array}{l}{50k+b=58}\\{100k+b=118}\end{array}\right.$,
解这个方程组得$\left\{\begin{array}{l}{k=1.2}\\{b=2}\end{array}\right.$,
此时y与x的关系式是y=1.2x-2
∴y与x的关系式是y=$\left\{\begin{array}{l}{58(x≤50)}\\{1.2x-2(x>50)}\end{array}\right.$;
(3)∵70>50,
∴当y=70时,1.2x-2=70,
解得:x=60,
答:小聪家某,该月交上网费70元,该月上网时间是60小时.
点评 本题重点考查了一次函数图象和实际应用相结合的问题,要注意图象中的分段函数是解题的关键.

练习册系列答案
相关题目
9.下列方程组中,以$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$为解的二元一次方程组是( )
| A. | $\left\{\begin{array}{l}{x+y=1}\\{x-y=1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=1}\\{x-y=3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+y=3}\\{x-y=3}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=-1}\\{x-y=-3}\end{array}\right.$ |
 某几何体的三视图如图所示,则组成该几何体的小正方体的个数是5.
某几何体的三视图如图所示,则组成该几何体的小正方体的个数是5.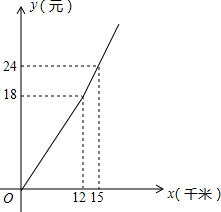 随着“互联网+”时代的到来,一种新型的打车方式受到大众欢迎.该打车方式采用阶梯收费标准.打车费用y(单位:元)与行驶里程x(单位:千米)的函数关系如图所示.如果小明某次打车行驶里程为20千米,则他的打车费用为( )
随着“互联网+”时代的到来,一种新型的打车方式受到大众欢迎.该打车方式采用阶梯收费标准.打车费用y(单位:元)与行驶里程x(单位:千米)的函数关系如图所示.如果小明某次打车行驶里程为20千米,则他的打车费用为( )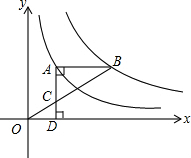 如图,点A在双曲线y=$\frac{3}{x}$上,点B在双曲线y=$\frac{k}{x}$(k≠0)上,AB∥x轴,过点A作AD⊥x轴于D,连接OB,与AD相交于点C,若AC=2CD,则k的值为9.
如图,点A在双曲线y=$\frac{3}{x}$上,点B在双曲线y=$\frac{k}{x}$(k≠0)上,AB∥x轴,过点A作AD⊥x轴于D,连接OB,与AD相交于点C,若AC=2CD,则k的值为9.