题目内容
3．不等式组$\left\{\begin{array}{l}{3x≥x-2}\\{\frac{x+1}{3}＞2x}\end{array}\right.$的解集-1≤x＜$\frac{1}{5}$．分析 分别求得不等式①②的解，然后取其公共部分即可得到不等式组的解集．
解答 解：∵不等式组$\left\{\begin{array}{l}{3x≥x-2①}\\{\frac{x+1}{3＞2x}②}\end{array}\right.$，
∴解①得：x≥-1，解②得：x＜$\frac{1}{5}$，
所以不等式组的解集为：-1≤x＜$\frac{1}{5}$，
故答案为：-1≤x＜$\frac{1}{5}$．
点评 本题主要考查了解一元一次不等式组的知识，要掌握解集的规律：同大取大；同小取小；大小小大中间找；大大小小找不到．
练习册系列答案
相关题目
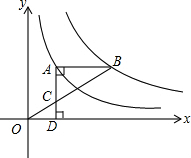如图，点A在双曲线y=$\frac{3}{x}$上，点B在双曲线y=$\frac{k}{x}$（k≠0）上，AB∥x轴，过点A作AD⊥x轴于D，连接OB，与AD相交于点C，若AC=2CD，则k的值为9．
在平面直角坐标系中指出下列各点A（5，1），B（5，0），C（2，1），D（2，3），并顺次连接，且将所得图形向下平移3个单位，写出对应点A′、B′、C′、D′的坐标．
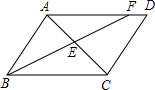如图，在?ABCD中，AB=2，BC=3，∠ABC的平分线BF分别与AC，AD交于点E，F，则$\frac{{S}_{△AEF}}{{S}_{△BEC}}$=$\frac{4}{9}$．
如图，边长为6的等边三角形ABC中，E是对称轴AD上的一个动点，连接EC，将线段EC绕点C逆时针旋转60°得到FC，连接DF．
13．下列说法中，正确的是（ ）
| A． | 方程$\sqrt{x}$=4的根是x=±16 | B． | 方程$\sqrt{3x}$=-x的根是x1=0，x2=3 | ||
| C． | 方程$\sqrt{x+1}$+1=0没有实数根 | D． | 方程3-$\sqrt{2x-3}$的根是x1=2，x2=6 |