题目内容
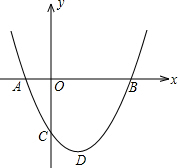 如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为-1,3.与y轴负半轴交于点C,在下面五个结论中:
如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为-1,3.与y轴负半轴交于点C,在下面五个结论中:①2a-b=0;②a+b+c>0;③c=-3a;④只有当a=
| 1 |
| 2 |
其中正确的结论是
考点:抛物线与x轴的交点,二次函数图象与系数的关系,等腰三角形的判定
专题:
分析:先根据图象与x轴的交点A,B的横坐标分别为-1,3确定出AB的长及对称轴,再由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答: 解:①∵图象与x轴的交点A,B的横坐标分别为-1,3,
解:①∵图象与x轴的交点A,B的横坐标分别为-1,3,
∴AB=4,
∴对称轴x=-
=1,
即2a+b=0.
故①错误;
②根据图示知,当x=1时,y<0,即a+b+c<0.
故②错误;
③∵A点坐标为(-1,0),
∴a-b+c=0,而b=-2a,
∴a+2a+c=0,即c=-3a.
故③正确;
④当a=
,则b=-1,c=-
,对称轴x=1与x轴的交点为E,如图,
∴抛物线的解析式为y=
x2-x-
,
把x=1代入得y=
-1-
=-2,
∴D点坐标为(1,-2),
∴AE=2,BE=2,DE=2,
∴△ADE和△BDE都为等腰直角三角形,
∴△ADB为等腰直角三角形.
故④正确;
⑤要使△ACB为等腰三角形,则必须保证AB=BC=4或AB=AC=4或AC=BC,
当AB=BC=4时,
∵AO=1,△BOC为直角三角形,
又∵OC的长即为|c|,
∴c2=16-9=7,
∵由抛物线与y轴的交点在y轴的负半轴上,
∴c=-
,
与2a+b=0、a-b+c=0联立组成解方程组,解得a=
;
同理当AB=AC=4时
∵AO=1,△AOC为直角三角形,
又∵OC的长即为|c|,
∴c2=16-1=15,
∵由抛物线与y轴的交点在y轴的负半轴上,
∴c=-
与2a+b=0、a-b+c=0联立组成解方程组,解得a=
;
同理当AC=BC时
在△AOC中,AC2=1+c2,
在△BOC中BC2=c2+9,
∵AC=BC,
∴1+c2=c2+9,此方程无解.
经解方程组可知只有两个a值满足条件.
故⑤错误.
综上所述,正确的结论是③④.
故答案是:③④.
 解:①∵图象与x轴的交点A,B的横坐标分别为-1,3,
解:①∵图象与x轴的交点A,B的横坐标分别为-1,3,∴AB=4,
∴对称轴x=-
| b |
| 2a |
即2a+b=0.
故①错误;
②根据图示知,当x=1时,y<0,即a+b+c<0.
故②错误;
③∵A点坐标为(-1,0),
∴a-b+c=0,而b=-2a,
∴a+2a+c=0,即c=-3a.
故③正确;
④当a=
| 1 |
| 2 |
| 3 |
| 2 |
∴抛物线的解析式为y=
| 1 |
| 2 |
| 3 |
| 2 |
把x=1代入得y=
| 1 |
| 2 |
| 3 |
| 2 |
∴D点坐标为(1,-2),
∴AE=2,BE=2,DE=2,
∴△ADE和△BDE都为等腰直角三角形,
∴△ADB为等腰直角三角形.
故④正确;
⑤要使△ACB为等腰三角形,则必须保证AB=BC=4或AB=AC=4或AC=BC,
当AB=BC=4时,
∵AO=1,△BOC为直角三角形,
又∵OC的长即为|c|,
∴c2=16-9=7,
∵由抛物线与y轴的交点在y轴的负半轴上,
∴c=-
| 7 |
与2a+b=0、a-b+c=0联立组成解方程组,解得a=
| ||
| 3 |
同理当AB=AC=4时
∵AO=1,△AOC为直角三角形,
又∵OC的长即为|c|,
∴c2=16-1=15,
∵由抛物线与y轴的交点在y轴的负半轴上,
∴c=-
| 15 |
与2a+b=0、a-b+c=0联立组成解方程组,解得a=
| ||
| 3 |
同理当AC=BC时
在△AOC中,AC2=1+c2,
在△BOC中BC2=c2+9,
∵AC=BC,
∴1+c2=c2+9,此方程无解.
经解方程组可知只有两个a值满足条件.
故⑤错误.
综上所述,正确的结论是③④.
故答案是:③④.
点评:本题考查了二次函数y=ax2+bx+c的图象与系数的关系:当a>0,抛物线开口向上;抛物线的对称轴为直线x=-
;抛物线与y轴的交点坐标为(0,c).
| b |
| 2a |

练习册系列答案
 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
若a2=10,则a=( )
| A、5 | ||
B、
| ||
C、±
| ||
| D、10 |
 如图,在△ABC中,∠ABC的平分线和∠ACB的外角平分线交于D,已知∠A=80°,则∠D=( )
如图,在△ABC中,∠ABC的平分线和∠ACB的外角平分线交于D,已知∠A=80°,则∠D=( )| A、40° | B、160° |
| C、120° | D、100° |
| 1 |
| 64 |
A、±
| ||
B、
| ||
C、±
| ||
D、
|
已知∠1与∠2互补,∠2与∠3互补,那么∠1与∠3的关系是( )
| A、相等 | B、互补 |
| C、互余 | D、不能确定 |
 如图,已知直角梯形ABCD的一条对角线把梯形分为一个直角三角形和一个以BC为底的等腰三角形.若梯形上底为5,则连接△DBC两腰中点的线段的长为
如图,已知直角梯形ABCD的一条对角线把梯形分为一个直角三角形和一个以BC为底的等腰三角形.若梯形上底为5,则连接△DBC两腰中点的线段的长为