题目内容
 如图,在△ABC中,∠ABC的平分线和∠ACB的外角平分线交于D,已知∠A=80°,则∠D=( )
如图,在△ABC中,∠ABC的平分线和∠ACB的外角平分线交于D,已知∠A=80°,则∠D=( )| A、40° | B、160° |
| C、120° | D、100° |
考点:三角形内角和定理,三角形的外角性质
专题:
分析:如图,利用三角形外角的性质和角平分线的性质得到∠2+
∠A=∠1.则∠1-∠2=40°.然后又由三角形外角性质推知∠D=∠1-∠2=40°.
| 1 |
| 2 |
解答: 解:如图,∵∠ABC+∠A=∠ACE,∠ABC的平分线和∠ACB的外角平分线交于D,
解:如图,∵∠ABC+∠A=∠ACE,∠ABC的平分线和∠ACB的外角平分线交于D,
∴
(∠ABC+∠A)=
∠ACE,即∠2+
∠A=∠1.
又∵∠A=80°,
∴∠2+40°=∠1,
∴∠1-∠2=40°
又∵∠2+∠D=∠1,
∴∠D=∠1-∠2=40°.
故选:A.
 解:如图,∵∠ABC+∠A=∠ACE,∠ABC的平分线和∠ACB的外角平分线交于D,
解:如图,∵∠ABC+∠A=∠ACE,∠ABC的平分线和∠ACB的外角平分线交于D,∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
又∵∠A=80°,
∴∠2+40°=∠1,
∴∠1-∠2=40°
又∵∠2+∠D=∠1,
∴∠D=∠1-∠2=40°.
故选:A.
点评:本题考查了三角形的外角性质:三角形的一个外角等于和它不相邻的两个内角的和.

练习册系列答案
相关题目
关于x的不等式(a-1)x>a-1的解集为x<1,则下列判断正确的是( )
| A、a<0 | B、a>1 |
| C、a<1 | D、a为任意数 |
计算
的值是( )
| (3-π)2 |
| A、3-π |
| B、-0.14 |
| C、π-3 |
| D、(3-π)2 |
若关于x,y的二元一次方程组
的解满足x-y<2,则a的取值范围是( )
|
| A、a>6 | B、a<6 |
| C、a>2 | D、a<2 |
 如图是小刚画的一张脸,他对妹妹说:如果我用(0,2)表示左眼,用(2,2)表示右眼,那么嘴的位置可以表示成
如图是小刚画的一张脸,他对妹妹说:如果我用(0,2)表示左眼,用(2,2)表示右眼,那么嘴的位置可以表示成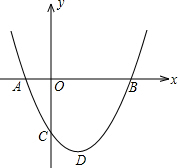 如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为-1,3.与y轴负半轴交于点C,在下面五个结论中:
如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为-1,3.与y轴负半轴交于点C,在下面五个结论中: 如图,在等腰直角△ABC中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P.则下列结论:
如图,在等腰直角△ABC中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P.则下列结论: